
【题目】定义:点C在线段AB上,若BC=![]() AC,则称点C是线段AB的一个圆周率点.
AC,则称点C是线段AB的一个圆周率点.
如图,已知点C是线段AB的一个靠近点A的圆周率点,AC=3.
(1)AB= ;(结果用含![]() 的代数式表示)
的代数式表示)
(2)若点D是线段AB的另一个圆周率点(不同于点C),则CD= ;
(3)若点E在线段AB的延长线上,且点B是线段CE的一个圆周率点.求出BE的长.
![]()
 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】某体育用品商场采购员要到厂家批发购买篮球和排球共![]() 个,篮球个数不少于排球个数,付款总额不得超过
个,篮球个数不少于排球个数,付款总额不得超过![]() 元,已知两种球厂的批发价和商场的零售价如下表. 设该商场采购
元,已知两种球厂的批发价和商场的零售价如下表. 设该商场采购![]() 个篮球.
个篮球.
品名 | 厂家批发价/元/个 | 商场零售价/元/个 |
篮球 |
|
|
排球 |
|
|
(1)求该商场采购费用![]() (单位:元)与
(单位:元)与![]() (单位:个)的函数关系式,并写出自变最
(单位:个)的函数关系式,并写出自变最![]() 的取值范围:
的取值范围:
(2)该商场把这![]() 个球全都以零售价售出,求商场能获得的最大利润;
个球全都以零售价售出,求商场能获得的最大利润;
(3)受原材料和工艺调整等因素影响,采购员实际采购时,低球的批发价上调了![]() 元/个,同时排球批发价下调了
元/个,同时排球批发价下调了![]() 元/个.该体有用品商场决定不调整商场零售价,发现将
元/个.该体有用品商场决定不调整商场零售价,发现将![]() 个球全部卖出获得的最低利润是
个球全部卖出获得的最低利润是![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以Rt△ABC的直角边AB为直径作圆O,与斜边交于点D,E为BC边上的中点,连接DE.
(1)求证:DE是⊙O的切线;
(2)连接OE,AE,当∠CAB为何值时,四边形AOED是平行四边形?并在此条件下求sin∠CAE的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点 P(-2,4)关于 y 轴的对称点 P'在反比例函数 y=![]() (k≠0)的图象上.
(k≠0)的图象上.
(1)求此反比例函数关系式;
(2)当 x 在什么范围取值时,y 是小于 1 的正数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角形 AEF 的顶点 E 在等腰直角三角形 ABC 的边 BC上.AB 的延长线交 EF 于 D 点,其中∠AEF=∠ABC=90°.
(1)求证:![]()
(2)若 E 为 BC 的中点,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
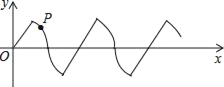
【题目】如图在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为每秒2个单位长度,点在弧线上的速度为每秒![]() 个单位长度,则2018秒时,点P的坐标是( )
个单位长度,则2018秒时,点P的坐标是( )
A. (2017,0) B. (2017, ![]() ) C. (2018,0) D. (2019,﹣
) C. (2018,0) D. (2019,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-2x+6与x轴交于点A,与直线y=x交于点B.
(1)点A坐标为_____________.
(2)动点M从原点O出发,以每秒1个单位长度的速度沿着O→A的路线向终点A匀速运动,过点M作MP⊥x轴交直线y=x于点P,然后以MP为直角边向右作等腰直角△MPN.设运动t秒时,ΔMPN与ΔOAB重叠部分的面积为S.求S与t之间的函数关系式,并直接写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
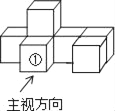
A. 主视图改变,俯视图改变 B. 左视图改变,俯视图改变
C. 俯视图不变,左视图改变 D. 主视图不变,左视图不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com