
【题目】请阅读下列材料:
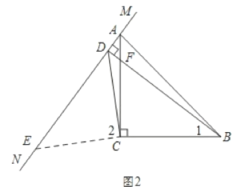
问题:如图1,△ABC中,∠ACB=90°,AC=BC,MN是过点A的直线,DB⊥MN于点D,联结CD.求证:BD+AD=![]() CD.
CD.
小明的思考过程如下:要证BD+AD=![]() CD,需要将BD,AD转化到同一条直线上,可以在MN上截取AE=BD,并联结EC,可证△ACE和△BCD全等,得到CE=CD,且∠ACE=∠BCD,由此推出△CDE为等腰直角三角形,可知DE=
CD,需要将BD,AD转化到同一条直线上,可以在MN上截取AE=BD,并联结EC,可证△ACE和△BCD全等,得到CE=CD,且∠ACE=∠BCD,由此推出△CDE为等腰直角三角形,可知DE=![]() CD,于是结论得证。
CD,于是结论得证。
小聪的思考过程如下:要证BD+AD=![]() CD,需要构造以CD为腰的等腰直角三角形,可以过点C作CE⊥CD交MN于点E,可证△ACE和△BCD全等,得到CE=CD,且AE=BD,由此推出△CDE为等腰直角三角形,可知DE=
CD,需要构造以CD为腰的等腰直角三角形,可以过点C作CE⊥CD交MN于点E,可证△ACE和△BCD全等,得到CE=CD,且AE=BD,由此推出△CDE为等腰直角三角形,可知DE=![]() CD,于是结论得证。
CD,于是结论得证。
请你参考小明或小聪的思考过程解决下面的问题:
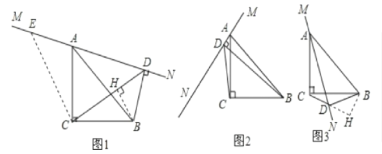
(1)将图1中的直线MN绕点A旋转到图2和图3的两种位置时,其它条件不变,猜想BD,AD,CD之间的数量关系,并选择其中一个图形加以证明;
(2)在直线MN绕点A旋转的过程中,当∠BCD=30°,BD=![]() 时,CD=___.
时,CD=___.

【答案】(1)BDAD=![]() CD.,证明见解析;(2)
CD.,证明见解析;(2)![]() ±1.
±1.
【解析】
(1)过点C作CE⊥CB于点C,与MN交于点E,证明△ACE≌△DCB,则△ECB为等腰直角三角形,据此即可得到BE=![]() CB,根据BE=AB-AE即可证得;
CB,根据BE=AB-AE即可证得;
(2)过点B作BH⊥CD于点H,证明△BDH是等腰直角三角形,求得DH的长,在直角△BCH中,利用直角三角形中30°的锐角所对的直角边等于斜边的一半,即可求得.
(1)如图2,过点C作CE⊥CD交MN于点E,则∠2=90°.
∵∠ACB=90°,∴∠2+∠ACD=∠ACB+∠ACD,
即∠ACE=∠BCD.
设AC与BD相交于点F,∵DB⊥MN,∴∠ADB=90°.
∴∠CAE+∠AFD=90°,∠1+∠BFC=90°.
∵∠AFD=∠BFC,∴∠CAE=∠1.
在△ACE和△BCD中
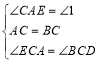 ,
,
∴△ACE≌△BCD(ASA).
∴CE=CD,AE=BD.
在Rt△CDE中,∵CD![]() +CE
+CE![]() =DE
=DE![]() ,
,
∴2CD![]() =DE
=DE![]() ,即DE=
,即DE=![]() CD.
CD.
∵DE=AEAD=BDAD,∴BDAD=![]() CD.
CD.
(2)MN在绕点A旋转过程中,这个的意思并没有指明是哪种情况,
∴综合了第一个图和第二个图两种情况
若是第1个图:易证△ACE≌△DCB,CE=CD,
∴△ECD为等腰直角三角形,
∴∠AEC=45°=∠CBD,
过D作DH⊥CB.则△DHB为等腰直角三角形。
BD=![]() BH,
BH,
∴BH=DH=1
直角三角形△CDH中,
∠DCH=30°,
BH=1,则CH=![]() .
.
∴CD=![]() +1
+1
若是第二个图:过B作BH⊥CD交CD延长于H.
解法类似上面,CH=![]() ,DH=1,CD=
,DH=1,CD=![]() 1.
1.
故答案为:![]() ±1.
±1.


科目:初中数学 来源: 题型:
【题目】如图,在边长都为a的正方形内分别排列着一些大小相等的圆.

(1)根据图中的规律,第4个正方形内圆的个数是 ,第n个正方形内圆的个数是 .
(2)如果把正方形内除去圆的部分都涂上阴影.
①用含a的代数式分别表示第1个正方形中和第3个正方形中阴影部分的面积.(结果保留π)
②若a=10,请直接写出第2014个正方形中阴影部分的面积 .(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的计算程序,并回答问题.
![]()
(1)填写表格
输入 |
| |
|
| … |
输出答案 | _____ | _____ | _____ | _____ | … |
(2)请写出你发现的规律;
(3)用简要过程说明你发现的规律的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在社会主义新农村建设中,某乡镇决定对一段公路进行改造,已知这项工程由甲工程队单独做需要40天完成;如果由乙工程先单独做10天,那么剩下的工程还需要两队合做20天才能完成.
(1)求乙工程队单独完成这项工程所需的天数;
(2)求两队合作完成这项工程所需的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
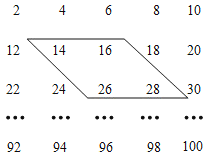
【题目】如图,数阵是由50个偶数排成的.
(1)在数阵中任意做一类似于图中的框,设其中最小的数为x,那么其他3个数怎样表示?
(2)如果这四个数的和是172,能否求出这四个数?
(3)如果扩充数阵的数据,框中的四个数的和可以是2019吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题
(1)如图1,已知点A、B、C,直线l及l上一点M,请你按照下列要求画出图形.
①画射线BM
②画线段AC
③请在直线l上确定一点O,使点O到点A与点B的距离之和(OA+OB)最小
(2)有5个大小一样的正方形制成的如图2所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(只需添加一个符合要求的正方形即可,并用阴影表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
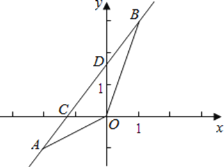
【题目】如图,已知一次函数y=kx+b的图象经过A(﹣2,﹣1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求该一次函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com