
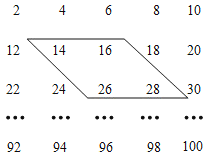
【题目】如图,数阵是由50个偶数排成的.
(1)在数阵中任意做一类似于图中的框,设其中最小的数为x,那么其他3个数怎样表示?
(2)如果这四个数的和是172,能否求出这四个数?
(3)如果扩充数阵的数据,框中的四个数的和可以是2019吗?为什么?
【答案】(1)设其中最小的数为x,则另外三个数分别为x+2,x+12,x+14.(2)这四个数分别为36,38,48,50.(3)不可以,理由见解析.
【解析】
(1)设其中最小的数为x,观察数阵可得出另外三个数分别为![]() ;
;
(2)由(1)的结论结合四个数之和为172,即可得出关于![]() 的一元一次方程,解之即可得出结论;
的一元一次方程,解之即可得出结论;
(3)由(1)的结论结合四个数之和为2019,即可得出关于![]() 的一元一次方程,解之即可得出
的一元一次方程,解之即可得出![]() 的值,由该值不为偶数,即可得出框中的四个数的和不可以是2019.
的值,由该值不为偶数,即可得出框中的四个数的和不可以是2019.
(1)设其中最小的数为x,则另外三个数分别为x+2,x+12,x+14.
(2)依题意,得:x+x+2+x+12+x+14=172,
解得:x=36,
∴x+2=38,x+12=48,x+14=50.
答:这四个数分别为36,38,48,50.
(3)不可以,理由如下:
依题意,得:x+x+2+x+12+x+14=2019,
解得:x=497![]() .
.
∵x为偶数,
∴不符合题意,即框中的四个数的和不可以是2019.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】点 P(-2,4)关于 y 轴的对称点 P'在反比例函数 y=![]() (k≠0)的图象上.
(k≠0)的图象上.
(1)求此反比例函数关系式;
(2)当 x 在什么范围取值时,y 是小于 1 的正数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
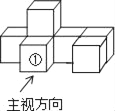
A. 主视图改变,俯视图改变 B. 左视图改变,俯视图改变
C. 俯视图不变,左视图改变 D. 主视图不变,左视图不变
查看答案和解析>>
科目:初中数学 来源: 题型:
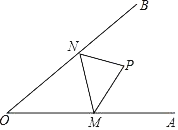
【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:如图1,△ABC中,∠ACB=90°,AC=BC,MN是过点A的直线,DB⊥MN于点D,联结CD.求证:BD+AD=![]() CD.
CD.
小明的思考过程如下:要证BD+AD=![]() CD,需要将BD,AD转化到同一条直线上,可以在MN上截取AE=BD,并联结EC,可证△ACE和△BCD全等,得到CE=CD,且∠ACE=∠BCD,由此推出△CDE为等腰直角三角形,可知DE=
CD,需要将BD,AD转化到同一条直线上,可以在MN上截取AE=BD,并联结EC,可证△ACE和△BCD全等,得到CE=CD,且∠ACE=∠BCD,由此推出△CDE为等腰直角三角形,可知DE=![]() CD,于是结论得证。
CD,于是结论得证。
小聪的思考过程如下:要证BD+AD=![]() CD,需要构造以CD为腰的等腰直角三角形,可以过点C作CE⊥CD交MN于点E,可证△ACE和△BCD全等,得到CE=CD,且AE=BD,由此推出△CDE为等腰直角三角形,可知DE=
CD,需要构造以CD为腰的等腰直角三角形,可以过点C作CE⊥CD交MN于点E,可证△ACE和△BCD全等,得到CE=CD,且AE=BD,由此推出△CDE为等腰直角三角形,可知DE=![]() CD,于是结论得证。
CD,于是结论得证。
请你参考小明或小聪的思考过程解决下面的问题:
(1)将图1中的直线MN绕点A旋转到图2和图3的两种位置时,其它条件不变,猜想BD,AD,CD之间的数量关系,并选择其中一个图形加以证明;
(2)在直线MN绕点A旋转的过程中,当∠BCD=30°,BD=![]() 时,CD=___.
时,CD=___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.

(1)已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC=10cm,BC=16cm,AD⊥BC于D,点E、F分别从B、C两点同时出发,其中点E沿BC向终点C运动,速度为4cm/s;点F沿CA、AB向终点B运动,速度为5cm/s,设它们运动的时间为x(s).
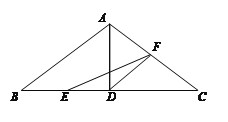
(1)求x为何值时,△EFC和△ACD相似;
(2)是否存在某一时刻,使得△EFD被 AD分得的两部分面积之比为3:5,若存在,求出x的值,若不存在,请说明理由;
(3)若以EF为直径的圆与线段AC只有一个公共点,求出相应x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
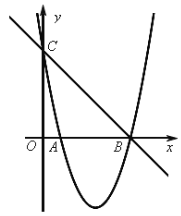
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com