
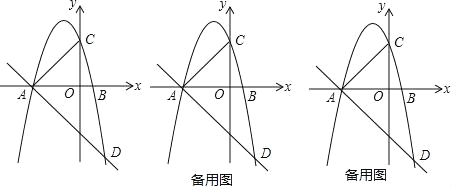
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏy=aΘ®x+3Θ©Θ®x©¹1Θ©Θ®aΓΌ0Θ©Θ§”κx÷α¥”Ήσ÷Ν”““ά¥ΈœύΫΜ”ΎAΓΔBΝΫΒψΘ§”κy÷αœύΫΜ”ΎΒψCΘ§Ψ≠ΙΐΒψAΒΡ÷±œΏy=©¹![]() x+b”κ≈ΉΈοœΏΒΡΝμ“ΜΗωΫΜΒψΈΣDΘ°
x+b”κ≈ΉΈοœΏΒΡΝμ“ΜΗωΫΜΒψΈΣDΘ°
Θ®1Θ©»τΒψDΒΡΚαΉχ±ξΈΣ2Θ§«σ≈ΉΈοœΏΒΡΚ· ΐΫβΈω ΫΘΜ
Θ®2Θ©»τ‘ΎΒΎ»ΐœσœόΡΎΒΡ≈ΉΈοœΏ…œ”–ΒψPΘ§ ΙΒΟ“‘AΓΔBΓΔPΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςABCœύΥΤΘ§«σΒψPΒΡΉχ±ξΘΜ
Θ®3Θ©‘ΎΘ®1Θ©ΒΡΧθΦΰœ¬Θ§…ηΒψE «œΏΕΈAD…œΒΡ“ΜΒψΘ®≤ΜΚ§ΕΥΒψΘ©Θ§Ν§Ϋ”BEΘ°“ΜΕ·ΒψQ¥”ΒψB≥ωΖΔΘ§―ΊœΏΕΈBE“‘ΟΩΟκ1ΗωΒΞΈΜΒΡΥΌΕ»‘ΥΕ·ΒΫΒψEΘ§‘Ό―ΊœΏΕΈED“‘ΟΩΟκ![]() ΗωΒΞΈΜΒΡΥΌΕ»‘ΥΕ·ΒΫΒψDΚσΆΘ÷ΙΘ§Έ Β±ΒψEΒΡΉχ±ξ «Εύ…Ό ±Θ§ΒψQ‘Ύ’ϊΗω‘ΥΕ·Ιΐ≥Χ÷–Υυ”Ο ±ΦδΉν…ΌΘΩ
ΗωΒΞΈΜΒΡΥΌΕ»‘ΥΕ·ΒΫΒψDΚσΆΘ÷ΙΘ§Έ Β±ΒψEΒΡΉχ±ξ «Εύ…Ό ±Θ§ΒψQ‘Ύ’ϊΗω‘ΥΕ·Ιΐ≥Χ÷–Υυ”Ο ±ΦδΉν…ΌΘΩ
ΓΨ¥πΑΗΓΩ(1) y=©¹![]() x2©¹2
x2©¹2![]() x+3
x+3![]() ΘΜ(2) PΒΡΉχ±ξΈΣΘ®©¹4Θ§©¹
ΘΜ(2) PΒΡΉχ±ξΈΣΘ®©¹4Θ§©¹![]() Θ©ΚΆΘ®©¹6Θ§©¹
Θ©ΚΆΘ®©¹6Θ§©¹![]() Θ©ΘΜ(3) Θ®1Θ§©¹4
Θ©ΘΜ(3) Θ®1Θ§©¹4![]() Θ©.
Θ©.
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨίΕΰ¥ΈΚ· ΐΒΡΫΜΒψ Ϋ»ΖΕ®ΒψAΓΔBΒΡΉχ±ξΘ§«σ≥ω÷±œΏΒΡΫβΈω ΫΘ§«σ≥ωΒψDΒΡΉχ±ξΘ§«σ≥ω≈ΉΈοœΏΒΡΫβΈω ΫΘΜΘ®2Θ©ΉςPHΓΆx÷α”ΎHΘ§…ηΒψPΒΡΉχ±ξΈΣΘ®mΘ§nΘ©Θ§Ζ÷ΓςBPAΓΉΓςABCΚΆΓςPBAΓΉΓςABCΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΦΤΥψΦ¥Ω…ΘΜΘ®3Θ©ΉςDMΓΈx÷αΫΜ≈ΉΈοœΏ”ΎMΘ§ΉςDNΓΆx÷α”ΎNΘ§ΉςEFΓΆDM”ΎFΘ§ΗυΨί’ΐ«–ΒΡΕ®“ε«σ≥ωQΒΡ‘ΥΕ· ±Φδt=BE+EF ±Θ§tΉν–ΓΦ¥Ω…Θ°
‘ΧβΫβΈωΘΚΘ®1Θ©ΓΏy=aΘ®x+3Θ©Θ®x©¹1Θ©Θ§
ΓύΒψAΒΡΉχ±ξΈΣΘ®©¹3Θ§0Θ©ΓΔΒψBΝΫΒΡΉχ±ξΈΣΘ®1Θ§0Θ©Θ§
ΓΏ÷±œΏy=©¹![]() x+bΨ≠ΙΐΒψAΘ§
x+bΨ≠ΙΐΒψAΘ§
Γύb=©¹3![]() Θ§
Θ§
Γύy=©¹![]() x©¹3
x©¹3![]() Θ§
Θ§
Β±x=2 ±Θ§y=©¹5![]() Θ§
Θ§
‘ρΒψDΒΡΉχ±ξΈΣΘ®2Θ§©¹5![]() Θ©Θ§
Θ©Θ§
ΓΏΒψD‘Ύ≈ΉΈοœΏ…œΘ§
ΓύaΘ®2+3Θ©Θ®2©¹1Θ©=©¹5![]() Θ§
Θ§
ΫβΒΟΘ§a=©¹![]() Θ§
Θ§
‘ρ≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=©¹![]() Θ®x+3Θ©Θ®x©¹1Θ©=©¹
Θ®x+3Θ©Θ®x©¹1Θ©=©¹![]() x2©¹2
x2©¹2![]() x+3
x+3![]() ΘΜ
ΘΜ
Θ®2Θ©ΉςPHΓΆx÷α”ΎHΘ§
…ηΒψPΒΡΉχ±ξΈΣΘ®mΘ§nΘ©Θ§
Β±ΓςBPAΓΉΓςABC ±Θ§ΓœBAC=ΓœPBAΘ§
ΓύtanΓœBAC=tanΓœPBAΘ§Φ¥![]() =
=![]() Θ§
Θ§
Γύ![]() =
=![]() Θ§Φ¥n=©¹aΘ®m©¹1Θ©Θ§
Θ§Φ¥n=©¹aΘ®m©¹1Θ©Θ§
Γύ![]() Θ§
Θ§
ΫβΒΟΘ§m1=©¹4Θ§m2=1Θ®≤ΜΚœΧβ“βΘ§…α»ΞΘ©Θ§
Β±m=©¹4 ±Θ§n=5aΘ§
ΓΏΓςBPAΓΉΓςABCΘ§
Γύ![]() =
=![]() ȧ֥AB2=ACPBȧ
ȧ֥AB2=ACPBȧ
Γύ42=![]()
![]() Θ§
Θ§
ΫβΒΟΘ§a1=![]() Θ®≤ΜΚœΧβ“βΘ§…α»ΞΘ©Θ§a2=©¹
Θ®≤ΜΚœΧβ“βΘ§…α»ΞΘ©Θ§a2=©¹![]() Θ§
Θ§
‘ρn=5a=©¹![]() Θ§
Θ§
ΓύΒψPΒΡΉχ±ξΈΣΘ®©¹4Θ§©¹![]() Θ©ΘΜ
Θ©ΘΜ
Β±ΓςPBAΓΉΓςABC ±Θ§ΓœCBA=ΓœPBAΘ§
ΓύtanΓœCBA=tanΓœPBAΘ§Φ¥![]() =
=![]() Θ§
Θ§
Γύ![]() =
=![]() Θ§Φ¥n=©¹3aΘ®m©¹1Θ©Θ§
Θ§Φ¥n=©¹3aΘ®m©¹1Θ©Θ§
Γύ![]() Θ§
Θ§
ΫβΒΟΘ§m1=©¹6Θ§m2=1Θ®≤ΜΚœΧβ“βΘ§…α»ΞΘ©Θ§
Β±m=©¹6 ±Θ§n=21aΘ§
ΓΏΓςPBAΓΉΓςABCΘ§
Γύ![]() =
=![]() ȧ֥AB2=BCPBȧ
ȧ֥AB2=BCPBȧ
Γύ42=![]()
![]() Θ§
Θ§
ΫβΒΟΘ§a1=![]() Θ®≤ΜΚœΧβ“βΘ§…α»ΞΘ©Θ§a2=©¹
Θ®≤ΜΚœΧβ“βΘ§…α»ΞΘ©Θ§a2=©¹![]() Θ§
Θ§
‘ρΒψPΒΡΉχ±ξΈΣΘ®©¹6Θ§©¹![]() Θ©Θ§
Θ©Θ§
Ήέ…œΥυ ωΘ§ΖϊΚœΧθΦΰΒΡΒψPΒΡΉχ±ξΈΣΘ®©¹4Θ§©¹![]() Θ©ΚΆΘ®©¹6Θ§©¹
Θ©ΚΆΘ®©¹6Θ§©¹![]() Θ©ΘΜ
Θ©ΘΜ
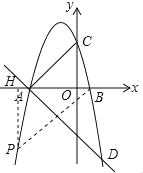
Θ®3Θ©ΉςDMΓΈx÷αΫΜ≈ΉΈοœΏ”ΎMΘ§ΉςDNΓΆx÷α”ΎNΘ§ΉςEFΓΆDM”ΎFΘ§
‘ρtanΓœDAN=![]() =
=![]() =
=
ΓύΓœDAN=60ΓψΘ§
ΓύΓœEDF=60ΓψΘ§
ΓύDE=![]() =
=![]() EFȧ
EFȧ
ΓύQΒΡ‘ΥΕ· ±Φδt=![]() +
+![]() =BE+EFȧ
=BE+EFȧ
ΓύΒ±BEΚΆEFΙ≤œΏ ±Θ§tΉν–ΓΘ§
‘ρBEΓΆDMΘ§E(1,©¹4![]() )Θ°
)Θ°


 –Γ―ßΩΈΧΟΉς“ΒœΒΝ–¥πΑΗ
–Γ―ßΩΈΧΟΉς“ΒœΒΝ–¥πΑΗ Ϋπ≤© Ω“ΜΒψ»ΪΆ®œΒΝ–¥πΑΗ
Ϋπ≤© Ω“ΜΒψ»ΪΆ®œΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΚ· ΐy=4-3x÷–Θ§yΥφxΒΡ‘ω¥σΕχ__________Θ§¥ΥΚ· ΐΆΦœσΨ≠Ιΐ________œσœόΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
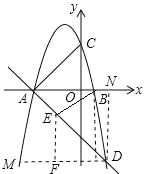
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ≈ΉΈοœΏ”κx÷αΫΜ”ΎAΘ®©¹1Θ§0Θ©Θ§BΘ®4Θ§0Θ©Θ§”κy÷αΫΜ”ΎCΘ®0Θ§©¹2Θ©Θ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©H «CΙΊ”Ύx÷αΒΡΕ‘≥ΤΒψΘ§P «≈ΉΈοœΏ…œΒΡ“ΜΒψΘ§Β±ΓςPBH”κΓςAOCœύΥΤ ±Θ§«σΖϊΚœΧθΦΰΒΡPΒψΒΡΉχ±ξΘ®«σ≥ωΝΫΒψΦ¥Ω…Θ©ΘΜ
Θ®3Θ©ΙΐΒψCΉςCDΓΈABΘ§CDΫΜ≈ΉΈοœΏ”ΎΒψDΘ§ΒψM «œΏΕΈCD…œΒΡ“ΜΕ·ΒψΘ§Ής÷±œΏMN”κœΏΕΈACΫΜ”ΎΒψNΘ§”κx÷αΫΜ”ΎΒψEΘ§«“ΓœBME=ΓœBDCΘ§Β±CNΒΡ÷ΒΉν¥σ ±Θ§«σΒψEΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
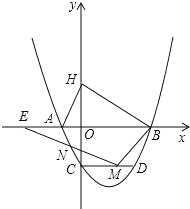
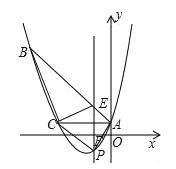
ΓΨΧβΡΩΓΩ(2016…ΫΕΪΈΪΖΜΒΎ25Χβ)»γΆΦΘ§“―÷Σ≈ΉΈοœΏy=![]() x2+bx+cΨ≠ΙΐΓςABCΒΡ»ΐΗωΕΞΒψΘ§Τδ÷–ΒψAΘ®0Θ§1Θ©Θ§ΒψBΘ®©¹9Θ§10Θ©Θ§ACΓΈx÷αΘ§ΒψP ±÷±œΏACœ¬ΖΫ≈ΉΈοœΏ…œΒΡΕ·ΒψΘ°
x2+bx+cΨ≠ΙΐΓςABCΒΡ»ΐΗωΕΞΒψΘ§Τδ÷–ΒψAΘ®0Θ§1Θ©Θ§ΒψBΘ®©¹9Θ§10Θ©Θ§ACΓΈx÷αΘ§ΒψP ±÷±œΏACœ¬ΖΫ≈ΉΈοœΏ…œΒΡΕ·ΒψΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜΘ®2Θ©ΙΐΒψP«“”κy÷αΤΫ––ΒΡ÷±œΏl”κ÷±œΏABΓΔACΖ÷±πΫΜ”ΎΒψEΓΔFΘ§Β±ΥΡ±Ώ–ΈAECPΒΡΟφΜΐΉν¥σ ±Θ§«σΒψPΒΡΉχ±ξΘΜ
Θ®3Θ©Β±ΒψPΈΣ≈ΉΈοœΏΒΡΕΞΒψ ±Θ§‘Ύ÷±œΏAC…œ «Ζώ¥φ‘ΎΒψQΘ§ ΙΒΟ“‘CΓΔPΓΔQΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςABCœύΥΤΘ§»τ¥φ‘ΎΘ§«σ≥ωΒψQΒΡΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
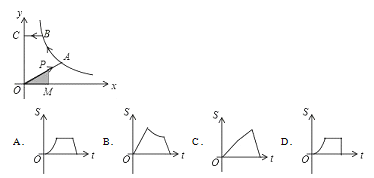
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣAΘ§B «Ζ¥±»άΐΚ· ΐy=![]() Θ®kΘΨ0Θ§xΘΨ0Θ©ΆΦœσ…œΒΡΝΫΒψΘ§BCΓΈx÷αΘ§ΫΜy÷α”ΎΒψCΘ§Ε·ΒψP¥”Ήχ±ξ‘≠ΒψO≥ωΖΔΘ§―ΊOΓζAΓζBΓζCΘ®ΆΦ÷–ΓΑΓζΓ±Υυ Ψ¬ΖœΏΘ©‘»ΥΌ‘ΥΕ·Θ§÷’ΒψΈΣCΘ§ΙΐPΉςPMΓΆx÷αΘ§¥ΙΉψΈΣMΘ°…η»ΐΫ«–ΈOMPΒΡΟφΜΐΈΣSΘ§PΒψ‘ΥΕ· ±ΦδΈΣtΘ§‘ρSΙΊ”ΎxΒΡΚ· ΐΆΦœσ¥σ÷¬ΈΣΘ® Θ©
Θ®kΘΨ0Θ§xΘΨ0Θ©ΆΦœσ…œΒΡΝΫΒψΘ§BCΓΈx÷αΘ§ΫΜy÷α”ΎΒψCΘ§Ε·ΒψP¥”Ήχ±ξ‘≠ΒψO≥ωΖΔΘ§―ΊOΓζAΓζBΓζCΘ®ΆΦ÷–ΓΑΓζΓ±Υυ Ψ¬ΖœΏΘ©‘»ΥΌ‘ΥΕ·Θ§÷’ΒψΈΣCΘ§ΙΐPΉςPMΓΆx÷αΘ§¥ΙΉψΈΣMΘ°…η»ΐΫ«–ΈOMPΒΡΟφΜΐΈΣSΘ§PΒψ‘ΥΕ· ±ΦδΈΣtΘ§‘ρSΙΊ”ΎxΒΡΚ· ΐΆΦœσ¥σ÷¬ΈΣΘ® Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
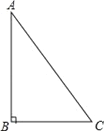
ΓΨΧβΡΩΓΩ“―÷ΣRtΓςABC÷–Θ§ΓœB=90ΓψΘ§
Θ®1Θ©ΗυΨί“Σ«σΉςΆΦΘ®≥ΏΙφΉςΆΦΘ§±ΘΝτΉςΆΦΚέΦΘΘ§≤Μ–¥Μ≠Ζ®Θ©ΘΚ
ΔΌΉςΓœBACΒΡΤΫΖ÷œΏADΫΜBC”ΎDΘΜ
ΔΎΉςœΏΕΈADΒΡ¥Ι÷±ΤΫΖ÷œΏΫΜAB”ΎEΘ§ΫΜAC”ΎFΘ§¥ΙΉψΈΣHΘΜ
ΔέΝ§Ϋ”EDΘ°
Θ®2Θ©‘ΎΘ®1Θ©ΒΡΜυ¥Γ…œ–¥≥ω“ΜΕ‘»ΪΒ»»ΐΫ«–ΈΘΚΓςΓΓ ΓΓΓ’ΓςΓΓ ΓΓ≤ΔΦ”“‘÷ΛΟςΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΫΪ÷±œΏy=2x-4œρ…œΤΫ“Τ5ΗωΒΞΈΜΚσΘ§ΥυΒΟ÷±œΏΒΡΫβΈω Ϋ « Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»ΥΒΡ¥σΡ‘ΟΩΧλΡήΦ«¬Φ¥σ‘Φ8 600ΆρΧθ–≈œΔΘ§ ΐΨί8 600”ΟΩΤ―ßΦ« ΐΖ®±μ ΨΈΣΘ® Θ©
A.0.86ΓΝ104
B.8.6ΓΝ102
C.8.6ΓΝ103
D.86ΓΝ102
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΒψA(1Θ§2aΘΪ3)‘ΎΒΎ“ΜœσœόΘ§«“ΒΫx÷αΒΡΨύάκ”κΒΫy÷αΒΡΨύάκœύΒ»Θ§‘ρaΘΫ________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com