
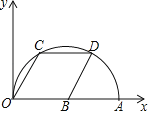
【题目】如图,在平面直角坐标系中,点A的坐标是(10,0),点C、D在以OA为直径的半圆上,点B在OA上,且四边形OCDB是菱形,则点C的坐标为_________.
【答案】(![]() ,
,![]() )
)
【解析】
根据题意连接AD,延长DC交y轴于M,连接AC,则∠OMC=90°,由菱形的性质得出OB=OC=CD=BD,OC∥BD,CD∥OB,∠BOC=∠BDC,得出∠BOC=∠ABD=∠BDC,由圆的两条平行弦的性质得出![]() ,由圆周角定理得出∠ACO=90°,得出OC=AD=BD=CD,OC⊥AC,证明△ABD是等边三角形,得出AB=BD=OB,∠BOC=∠ABD=60°,得出OC=OB=
,由圆周角定理得出∠ACO=90°,得出OC=AD=BD=CD,OC⊥AC,证明△ABD是等边三角形,得出AB=BD=OB,∠BOC=∠ABD=60°,得出OC=OB=![]() OA=5,由直角三角形的性质得出CM=
OA=5,由直角三角形的性质得出CM=![]() OC=
OC=![]() ,OM=
,OM=![]() CM=
CM=![]() ,即可得出答案.
,即可得出答案.
解:连接AD,延长DC交y轴于M,连接AC,如图所示:
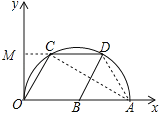
则∠OMC=90°,
∵四边形OCDB是菱形,
∴OB=OC=CD=BD,OC∥BD,CD∥OB,∠BOC=∠BDC,
∴∠BOC=∠ABD=∠BDC,
∵点C、D在以OA为直径的半圆上,CD∥OA,
∴![]() ,∠ACO=90°,
,∠ACO=90°,
∴OC=AD=BD=CD,OC⊥AC,
∴∠ABD=∠BAD,BD⊥AC,
∵CD=AD,
∴∠BDC=∠ADB,
∴∠ABD=∠BAD=∠ADB,
∴△ABD是等边三角形,
∴AB=BD=OB,∠BOC=∠ABD=60°,
∵点A的坐标是(10,0),
∴OA=10,
∴OC=OB=![]() OA=5,
OA=5,
∵∠OMC=90°,
∴∠COM=30°,
∴CM=![]() OC=
OC=![]() ,OM=
,OM=![]() CM=
CM=![]() ,
,
∴点C的坐标为(![]() ,
,![]() );
);
故答案为:(![]() ,
,![]() ).
).


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,探究函数图象和性质过程如下:
,探究函数图象和性质过程如下:
(1)下表是y与x的几组值,则解析式中的m= ,表格中的n= ;
x | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y |
|
|
| 1 |
| 3 |
| 4 |
| 3 | n | 0 | … |
(2)在平面直角坐标系中描出表格中各点,并画出函数图象:
(3)若A(x1,y1)、B(x2,y2)、C(x3,y3)为函数图象上的三个点,其中x2+x3>4且﹣1<x1<0<x2<2<x3<4,则y1、y2、y3之间的大小关系是 ;
(4)若直线y=k+1与该函数图象有且仅有一个交点,则k的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
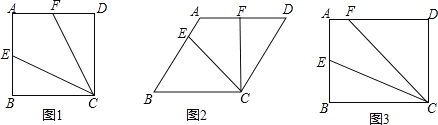
【题目】在四边形ABCD中,点E、F分别是AB、AD边上一点,∠DFC=2∠FCE.
(1)如图1,若四边形ABCD是正方形,∠DFC=60°,BE=4,则AF= .
(2)如图2,若四边形ABCD是菱形,∠A=120°,∠DFC=90°,BE=4,求![]() 的值.
的值.
(3)如图3,若四边形ABCD是矩形,点E是AB的中点,CE=12,CF=13,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】木工师傅可以用角尺测量并计算出圆的半径r.用角尺的较短边紧靠⊙O,角尺的顶点B(∠B=90°),并使较长边与⊙O相切于点C.

(1)如图,AB<r,较短边AB=8cm,读得BC长为12cm,则该圆的半径r为多少?
(2)如果AB=8cm,假设角尺的边BC足够长,若读得BC长为acm,则用含a的代数式表示r为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC的长为0.60m,底座BC与支架AC所成的角∠ACB=75°,点A、H、F在同一条直线上,支架AH段的长为1m,HF段的长为1.50m,篮板底部支架HE的长为0.75m.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板顶端F到地面的距离.(结果精确到0.1 m;参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
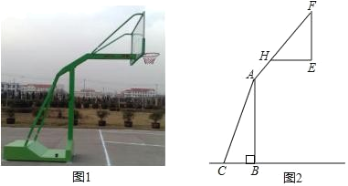
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5![]() 米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
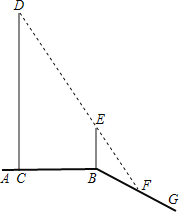
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据:
(1)由上表填空:a= ,b= ,c= ,d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过三点(1,0),(-6,0)(0,-3).
的图象经过三点(1,0),(-6,0)(0,-3).
(1)求该二次函数的解析式.
(2)若反比例函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象在第一象限内交于点A(
的图象在第一象限内交于点A(![]() ),
),![]() 落在两个相邻的正整数之间,请求出这两个相邻的正整数.
落在两个相邻的正整数之间,请求出这两个相邻的正整数.
(3)若反比例函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象在第一象限内的交点为B,点B的横坐标为m,且满足3<m<4,求实数k的取值范围.
的图象在第一象限内的交点为B,点B的横坐标为m,且满足3<m<4,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com