
【题目】如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5![]() 米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
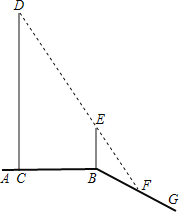
【答案】大树CD的高度为15.8米.
【解析】
延长CB交EF于点H,过点F作FM⊥EB的延长线于点M,在直角三角形MBF中,利用30°角的性质求出BM和MF,再利用相似求出BH长度;最后由△HBE∽△HCD,求出CD即大树的高度即可.
解:延长CB交EF于点H,过点F作FM⊥EB的延长线于点M,
∵∠ABG=150°,BE⊥CB,
∴∠MBF=150°﹣90°=60°,
∴∠MFB=30°,
∵BF的长为2米,
∴BM=1米,MF=![]() 米.
米.
∵BE⊥CB,MF⊥BE,
∴BH∥MF,
∴△EBH∽△EMF,
∴![]() =
=![]() .
.
又∵EB=1.8米,
∴![]() =
=![]() ,
,
∴BH=![]() .
.
∵BE∥CD,
∴△HBE∽△HCD,
∴![]() =
=![]() .
.
∵CB=5![]() ,
,
∴ =
=![]() ,
,
∴CD=15.8米.
∴大树CD的高度为15.8米.



科目:初中数学 来源: 题型:
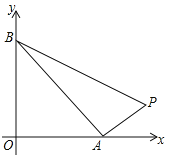
【题目】如图,由点P(14,1),A(![]() ,0),B(0,
,0),B(0,![]() )(
)(![]() ),确定的△PAB的面积为18,则
),确定的△PAB的面积为18,则![]() 的值为_________,如果
的值为_________,如果![]() ,则
,则![]() 的值为_____________________
的值为_____________________
查看答案和解析>>
科目:初中数学 来源: 题型:
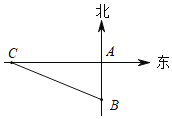
【题目】如图,一艘船以40km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的速度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区.当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km.
(1)如果这艘轮船不改变航向,经过9小时,轮船与台风中心相距多远?它此时是否受到台风影响?
(2)如果这艘轮船会受到台风影响,那么从接到警报开始,经过多长时间它就会进入台风影响区?
查看答案和解析>>
科目:初中数学 来源: 题型:
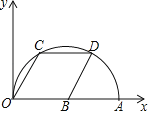
【题目】如图,在平面直角坐标系中,点A的坐标是(10,0),点C、D在以OA为直径的半圆上,点B在OA上,且四边形OCDB是菱形,则点C的坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
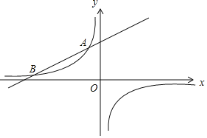
【题目】如图,反比例函数y=![]() 与一次函数y=ax+b的图象交于点A(﹣2,6)、点B(n,1).
与一次函数y=ax+b的图象交于点A(﹣2,6)、点B(n,1).
(1)求反比例函数与一次函数的表达式;
(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
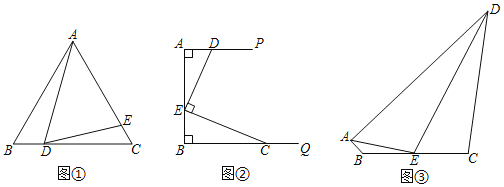
(1)如图①,在边长为8的等边三角形ABC中,点D,E分别在BC与AC上,且BD=2,∠ADE=60°,则线段CE的长为 .
问题
(2)如图②,已知AP∥BQ,∠A=∠B=90°,AB=6,D是射线AP上的一个动点(不与点A重合),E是线段AB上的一个动点(不与A,B重合),EC⊥DE,交射线BQ于点C,且AD+DE=AB,求△BCE的周长.
问题解决:
(3)如图③,在四边形ABCD中,AB+CD=10(AB<CD),BC=6,点E为BC的中点,且∠AED=108°,则边AD的长是否存在最大值?若存在,请求AD的最大值,并求出此时AB,CD的长度,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个定点坐标分别为A(﹣1,3),B(﹣1,1),C(﹣3,2).
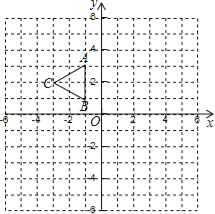
(1)请画出△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2,请在第三象限内画出△A2B2C2,并求出S△A1B1C1:S△A2B2C2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
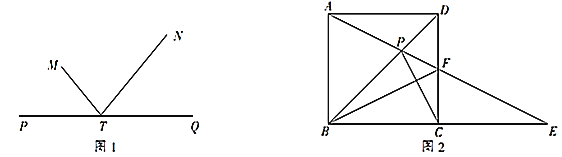
【题目】如图1,直线PQ的同侧有两点M,N,点T在直线PQ上,若∠MTP=∠NTQ,则称点M,N为关于直线PQ的衍射点.如图2,BD是矩形ABCD的对角线,E是边BC延长线上的一点,且CE=BC,连接AE交CD于点F,交BD于点P,连接BF,CP.
(1)求证:点A,B是关于直线CD的衍射点.
(2)若点C,F是关于直线BD的衍射点,CP=2PF=2![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).

(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(记过保留根号和π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com