
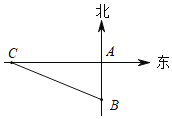
【题目】如图,一艘船以40km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的速度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区.当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km.
(1)如果这艘轮船不改变航向,经过9小时,轮船与台风中心相距多远?它此时是否受到台风影响?
(2)如果这艘轮船会受到台风影响,那么从接到警报开始,经过多长时间它就会进入台风影响区?
【答案】(1)轮船与台风中心相距40![]() km,它此时受到台风影响;(2)轮船经7小时就进入台风影响区
km,它此时受到台风影响;(2)轮船经7小时就进入台风影响区
【解析】
(1)根据勾股定理即可得到结论;
(2)首先假设轮船能进入台风影响区,进而利用勾股定理得出等式求出即可.
解:(1)∵∠CAB=90°,BC=500,AB=300,
∴AC=400km,
设经过9小时,轮船到达点F,且航行了40×9=360km,台风中心到达B′,且BG=20×9=180km,
∴CF=360,
∴AF=40,AG=120km,
∴![]()
∴轮船与台风中心相距40![]() km,它此时受到台风影响;
km,它此时受到台风影响;
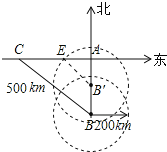
(2)如图所示:
设x小时后,就进入台风影响区,根据题意得出:
CE=30x千米,BB′=20x千米,
∵BC=500km,AB=300km,AC=400km,
∴AE=400﹣40x,AB′=300﹣20x,
∴AE2+AB′2=EB′2,
即(400﹣40x)2+(300﹣20x)2=2002,
解得:x1=15,x2=7,
∴轮船经7小时就进入台风影响区.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,按以下步骤作图:①以点A为圆心,AB的长为半径作弧,交AD于点F;②分别以点F,B为圆心大于![]() FB的长为半径作弧,两弧在∠DAB内交于点G;③作射线AG,交边BC于点E,连接EF.若AB=5,BF=8,则四边形ABEF的面积为( )
FB的长为半径作弧,两弧在∠DAB内交于点G;③作射线AG,交边BC于点E,连接EF.若AB=5,BF=8,则四边形ABEF的面积为( )

A.12B.20C.24D.48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
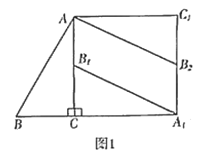
![]() 操作发现:如图1,在
操作发现:如图1,在![]() 中,
中,![]() ,以点
,以点![]() 为中心,把
为中心,把![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ;再以点
;再以点![]() 为中心,把
为中心,把![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() .连接
.连接![]() .则
.则![]() 与
与![]() 的位置关系为平行;
的位置关系为平行;
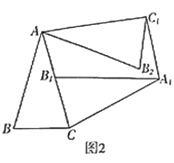
![]() 探究证明:如图2,当
探究证明:如图2,当![]() 是锐角三角形,
是锐角三角形,![]() 时,将
时,将![]() 按照(1)中的方式,以点
按照(1)中的方式,以点![]() 为中心,把
为中心,把![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ;再以点
;再以点![]() 为中心,把
为中心,把![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() .连接
.连接![]() ,
,
①探究![]() 与
与![]() 的位置关系,写出你的探究结论,并加以证明;
的位置关系,写出你的探究结论,并加以证明;
②探究![]() 与
与![]() 的位置关系,写出你的探究结论,并加以证明.
的位置关系,写出你的探究结论,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,同时点
匀速运动,同时点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,它们的速度均为
匀速运动,它们的速度均为![]() .作
.作![]() 于
于![]() ,连接
,连接![]() ,设运动时间为
,设运动时间为![]() ,解答下列问题:
,解答下列问题:
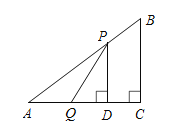
(1)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,
之间的函数关系式,![]() 的最大值是 ;
的最大值是 ;
(2)当![]() 的值为 时,
的值为 时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
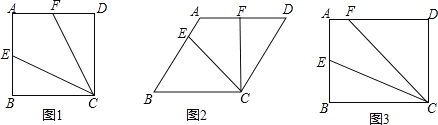
【题目】在四边形ABCD中,点E、F分别是AB、AD边上一点,∠DFC=2∠FCE.
(1)如图1,若四边形ABCD是正方形,∠DFC=60°,BE=4,则AF= .
(2)如图2,若四边形ABCD是菱形,∠A=120°,∠DFC=90°,BE=4,求![]() 的值.
的值.
(3)如图3,若四边形ABCD是矩形,点E是AB的中点,CE=12,CF=13,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】木工师傅可以用角尺测量并计算出圆的半径r.用角尺的较短边紧靠⊙O,角尺的顶点B(∠B=90°),并使较长边与⊙O相切于点C.

(1)如图,AB<r,较短边AB=8cm,读得BC长为12cm,则该圆的半径r为多少?
(2)如果AB=8cm,假设角尺的边BC足够长,若读得BC长为acm,则用含a的代数式表示r为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
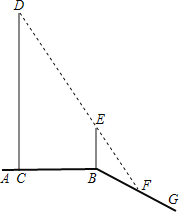
【题目】如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5![]() 米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
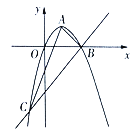
【题目】如图,在平面直角坐标系中,已知抛物线经过原点![]() ,顶点为
,顶点为![]() ,且与直线
,且与直线![]() 相交于
相交于![]() 两点.
两点.
(1)求抛物线的解析式;
(2)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(3)若点![]() 为
为![]() 轴上的一个动点,过点
轴上的一个动点,过点![]() 作
作![]() 轴与抛物线交于点
轴与抛物线交于点![]() ,则是否存在以
,则是否存在以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请直接写出点
相似?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com