
【题目】如图,△ABC三个定点坐标分别为A(﹣1,3),B(﹣1,1),C(﹣3,2).
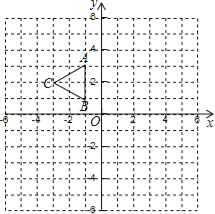
(1)请画出△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2,请在第三象限内画出△A2B2C2,并求出S△A1B1C1:S△A2B2C2的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】综合与探究:
![]() 操作发现:如图1,在
操作发现:如图1,在![]() 中,
中,![]() ,以点
,以点![]() 为中心,把
为中心,把![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ;再以点
;再以点![]() 为中心,把
为中心,把![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() .连接
.连接![]() .则
.则![]() 与
与![]() 的位置关系为平行;
的位置关系为平行;
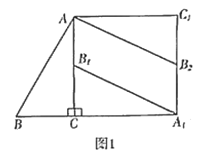
![]() 探究证明:如图2,当
探究证明:如图2,当![]() 是锐角三角形,
是锐角三角形,![]() 时,将
时,将![]() 按照(1)中的方式,以点
按照(1)中的方式,以点![]() 为中心,把
为中心,把![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ;再以点
;再以点![]() 为中心,把
为中心,把![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() .连接
.连接![]() ,
,
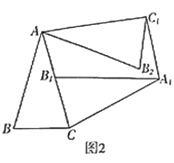
①探究![]() 与
与![]() 的位置关系,写出你的探究结论,并加以证明;
的位置关系,写出你的探究结论,并加以证明;
②探究![]() 与
与![]() 的位置关系,写出你的探究结论,并加以证明.
的位置关系,写出你的探究结论,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】木工师傅可以用角尺测量并计算出圆的半径r.用角尺的较短边紧靠⊙O,角尺的顶点B(∠B=90°),并使较长边与⊙O相切于点C.

(1)如图,AB<r,较短边AB=8cm,读得BC长为12cm,则该圆的半径r为多少?
(2)如果AB=8cm,假设角尺的边BC足够长,若读得BC长为acm,则用含a的代数式表示r为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
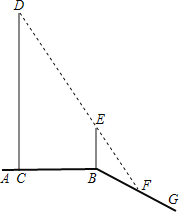
【题目】如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5![]() 米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
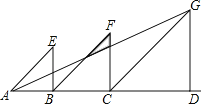
【题目】三个等腰直角三角形Rt△ABE,Rt△BCF,Rt△CDG如图摆放在射线AD上,直角顶点分别为B,C,D,已知相似比为2:3:4,AB=4,则(1)CG的长为_____;(2)图中阴影部分的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据:
(1)由上表填空:a= ,b= ,c= ,d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
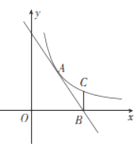
【题目】如图,反比例函数y=![]() (x>0)与直线AB交于点A(2,3),直线AB与x轴交于点B(4,0),过点B作x轴的垂线BC交反比例函数的图象于点C,在平面内有点D,使得以A,B,C,D四点为顶点的四边形为平行四边形,则平行四边形ABCD的面积为____________.
(x>0)与直线AB交于点A(2,3),直线AB与x轴交于点B(4,0),过点B作x轴的垂线BC交反比例函数的图象于点C,在平面内有点D,使得以A,B,C,D四点为顶点的四边形为平行四边形,则平行四边形ABCD的面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
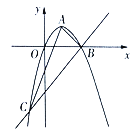
【题目】如图,在平面直角坐标系中,已知抛物线经过原点![]() ,顶点为
,顶点为![]() ,且与直线
,且与直线![]() 相交于
相交于![]() 两点.
两点.
(1)求抛物线的解析式;
(2)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(3)若点![]() 为
为![]() 轴上的一个动点,过点
轴上的一个动点,过点![]() 作
作![]() 轴与抛物线交于点
轴与抛物线交于点![]() ,则是否存在以
,则是否存在以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请直接写出点
相似?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
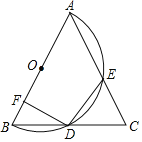
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆O,交BC于点D,交AC于点E.
(1)求证:BD=CD.
(2)若弧DE=50°,求∠C的度数.
(3)过点D作DF⊥AB于点F,若BC=8,AF=3BF,求弧BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com