
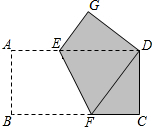
 如图,矩形ABCD中,AB=2,AD=4,将矩形沿FE折叠,使点B与点D重合,点A的对应点是点G,则图中阴影部分的面积为$\frac{11}{2}$.
如图,矩形ABCD中,AB=2,AD=4,将矩形沿FE折叠,使点B与点D重合,点A的对应点是点G,则图中阴影部分的面积为$\frac{11}{2}$. 分析 根据矩形的性质,可得BC与AD的关系,根据翻折的性质,AB与DG的关系,根据全等三角形的判定与性质,可得EG与CF的关系,根据勾股定理,可得CF的长,根据面积的和差,可得答案.
解答 解:∵四边形ABCD是矩形,
∴BC||AD,
∴∠BFE=∠DEF,
∵将矩形纸片沿EF折叠,使点B与点D重合,
∴∠BFE=∠EFD,
∴∠DEF=∠DFE,
∴DE=DF.
∵将矩形纸片沿EF折叠,使点B与点D重合,
∴DG=AB=2.
∵四边形ABCD是矩形,
∴AB=CD
∴DG=CD.
在Rt△CDF和Rt△DGE中,$\left\{\begin{array}{l}{∠GDE=∠CDF}\\{∠G=∠C=90°}\\{DG=CD}\end{array}\right.$,
∴△CDF∽△DGE,
∴EG=CF,DE=CF,
设BF=DF=x,则CF=EG=(4-x),
在Rt△CDF中,DF2=CF2+CD2,
即(4-x)2+22=x2
x=$\frac{5}{2}$,CF=$\frac{3}{2}$.
∵DE=BF=$\frac{5}{2}$,
∴AE=CF=$\frac{3}{2}$,
∴S着色=S四边形CDEF+S△DEG,
=$\frac{1}{2}$×($\frac{3}{2}$+$\frac{5}{2}$)×2+$\frac{1}{2}$×2×$\frac{3}{2}$
=4+$\frac{3}{2}$
=$\frac{11}{2}$.
故答案为:$\frac{11}{2}$.
点评 本题考查了翻折的性质,利用了矩形的性质,翻折的性质,利用勾股定理得出BE的长是解题关键,又利用了面积的和差.


科目:初中数学 来源: 题型:选择题
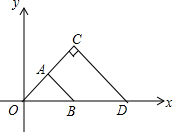 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则C点的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则C点的坐标为( )| A. | (1,2) | B. | ($\sqrt{2},\sqrt{2}$) | C. | (1,1) | D. | (2,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2x+1}$ | B. | $\frac{x}{2x+1}$ | C. | $\frac{3x+1}{{x}^{2}}$ | D. | $\frac{{x}^{2}}{2{x}^{2}+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把一张矩形纸片对折两次得到四个小矩形,如果每个小矩形都与原矩形相似,则原矩形纸片的长与宽之比为( )
如图,把一张矩形纸片对折两次得到四个小矩形,如果每个小矩形都与原矩形相似,则原矩形纸片的长与宽之比为( )| A. | $\sqrt{2}$:1 | B. | 2:1 | C. | 3:1 | D. | 4:1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
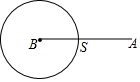 如图,动点S从点A出发,沿线段AB运动至点B后,立即按原路返回,点S在运动过程中速度不变,则以点B为圆心,线段BS长为半径的圆的面积m与点S的运动时间t之间的函数关系图象大致为( )
如图,动点S从点A出发,沿线段AB运动至点B后,立即按原路返回,点S在运动过程中速度不变,则以点B为圆心,线段BS长为半径的圆的面积m与点S的运动时间t之间的函数关系图象大致为( )| A. |  | B. |  | C. | 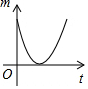 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com