
【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5m,EF=0.25m,目测点D到地面的距离DG=1.5m,到旗杆的水平距离DC=20m,则旗杆的高度为( )
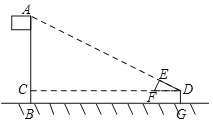
A.![]() mB.
mB.![]() m
m
C.11.5mD.10m
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】某课外学习小组根据学习函数的经验,对函数![]() 的图象与性质进行了探究请补充完整以下探索过程:
的图象与性质进行了探究请补充完整以下探索过程:
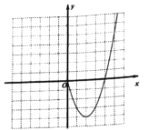
(1)列表:
x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | m | 0 | -3 | -4 | -3 | 0 | -3 | -4 | n | 0 | … |
直接写出![]() ________,
________,![]() ________;
________;
(2)根据上表中的数据,在平面直角坐标系内补全该函数的图象,并结合图象写出该函数的两条性质:
性质1______________________________________________________
性质2_______________________________________________________
(3)若方程![]() 有四个不同的实数根,请根据函数图象,直接写出k的取值范围.
有四个不同的实数根,请根据函数图象,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7
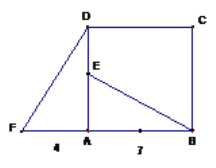
(1)指出旋转中心和旋转角度.
(2)求DE的长度.
(3)BE与DF垂直吗? 说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在边AB上,点E在边AC上,CE=BD,连接CD,BE,BE与CD相交于点F.
(1)如图1,若△ACD为等边三角形,且CE=DF,求∠CEF的度数;
(2)如图2,若AC=AD,求证:EF=FB;
(3)如图3,在(2)的条件下,若∠CFE=45°,△BCD的面积为4,求线段CD的长.
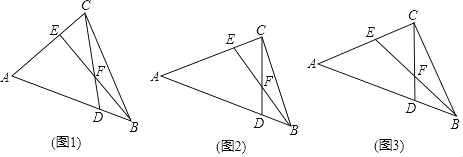
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备进一批季节性小家电,进价为每台40元,经市场预测,售价为每台48元时,可售出220台;售价每增加1元,销售量减少10台。
(1)当售价为55元,销售量为多少台?
(2)因受库存的影响,每批次进货个数不得超过160台,若商店想获得2000元利润,则应进货多少台?售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=40°,则∠ACB=( ).
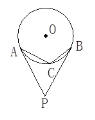
A.70°B.80°C.110°D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校同学组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):

(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是![]() 分2,则成绩较为整齐的是 队.
分2,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D、E是⊙O上的5等分点,连接AC、CE、EB、BD、DA,得到一个五角星图形和五边形MNFGH.有下列3个结论:① AO⊥BE, ② ∠CGD=∠COD+∠CAD, ③ BM=MN=NE.其中正确的结论是( )
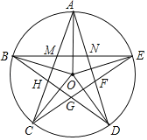
A.① ②B.① ③C.② ③D.① ② ③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com