
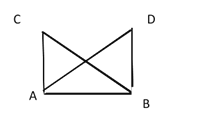
【题目】如图,海岸上有 A,B 两个观测点,点 B 在点 A 的正东方,海岛 C 在观测点 A 的正北方, 海岛 D 在观测点 B 的正北方。如果从观测点 A 看海岛 C,D 的视角∠CAD 与从观测点 B 海岛 C,D 的视角∠CBD 相等,那么海岛 C,D 到观测点 A,B 所在海岸的距离 CA,DB 相等,请说明理由。
科目:初中数学 来源: 题型:
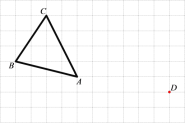
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF;
(2)请利用格点画出△ABC的高BM;
(3)△DEF的面积为 ;
(4)若连接AD、CF,则这两条线段之间的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有四个点A、B、C、D,点A在数轴上表示的数是-12,点D在数轴上表示的数是15, AB长2个单位长度,CD长1个单位长度.
![]()
(1)点B在数轴上表示的数是 ,点C的数轴上表示的数是 ,线段BC= .
(2)若点B以1个单位长度/秒的速度向右运动,同时点C以2个单位长度/秒的速度向左运动设运动时间为t秒,若BC长6个单位长度,求t的值;
(3)若线段AB以1个单位长度/秒的速度向左运动,同时线段CD以2个单位长度/秒的速度也向左运动.设运动时间为t秒.
①用含有t的式子分别表示点A、B、C、D,则A是 ,B是 ,C是 ,D是 .
②若0<t<24时,设M为AC中点,N为BD中点,试求出线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
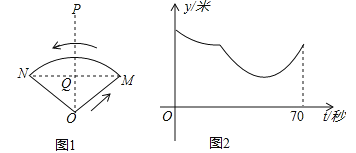
【题目】小阳在如图①所示的扇形舞台上沿O-M-N匀速行走,他从点O出发,沿箭头所示的方向经过点M再走到点N,共用时70秒.有一台摄像机选择了一个固定的位置记录了小阳的走路过程,设小阳走路的时间为t(单位:秒),他与摄像机的距离为y(单位:米),表示y与t的函数关系的图象大致如图②,则这个固定位置可能是图①中的点_______(在点P、N、Q、M、O中选取)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=ax2+bx+c, y与x的一些对应值如下表:
x | …… | 1 | 0 | 1 | 2 | 3 | 4 | …… |
ax2+bx+c | …… | 3 | 1 | 3 | …… |
(1)根据表格中的数据,确定二次函数解析式为_________________;
(2)填齐表格中空白处的对应值并利用上表,用五点作图法,画出二次函数y=ax2+bx+c的图象.(不必重新列表)
(3)当 1 < x ≤4时,y的取值范围是_________________;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究活动:
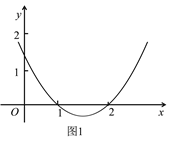
利用函数![]() 的图象(如图1)和性质,探究函数
的图象(如图1)和性质,探究函数![]() 的图象与性质.
的图象与性质.
下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;
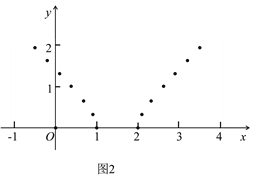
(2)如图2,小东列表描出了函数![]() 图象上部分点,请画出函数图象;
图象上部分点,请画出函数图象;
(3)解决问题:设方程![]() 的两根为
的两根为![]() 、
、![]() ,且
,且![]() ,方程
,方程
![]() 的两根为
的两根为![]() 、
、![]() ,且
,且![]() .若
.若![]() ,则
,则![]() 、
、![]() 、
、![]() 、
、![]() 的大小关系为_____________________(用“<”连接).
的大小关系为_____________________(用“<”连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
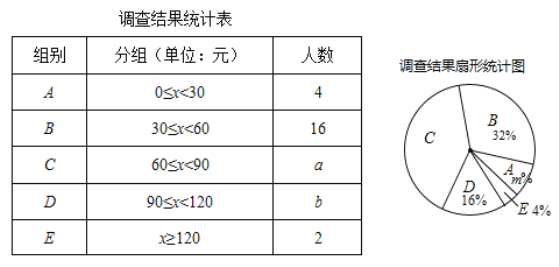
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__________人,a+b=__________,m=__________;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额在60≤x<120范围的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年春节期间,某物业公司组织两个小区的部分居民去旅游,已知某景点的门票价格如下表:
年春节期间,某物业公司组织两个小区的部分居民去旅游,已知某景点的门票价格如下表:
购票人数 |
|
|
|
每人门票价 |
|
|
|
小区①的人数少于![]() 人,小区②的人数多于
人,小区②的人数多于![]() 人且少于
人且少于![]() 人,如果两小区单独购票,则一共支付
人,如果两小区单独购票,则一共支付![]() 元;如果两小区联合起来作为一个团体购票,因为人数超过
元;如果两小区联合起来作为一个团体购票,因为人数超过![]() 人,只需花费
人,只需花费![]() 元请问:
元请问:
(1)两个小区各有多少人?
(2)团体购票与单独购票相比较,两个小区各节省了多少钱?
(3)若小区①单独购票,请为小区①设计一种最省钱的购买方案,并计算能省多少元钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
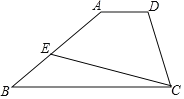
【题目】在四边形ABCD中,AD∥BC,E为AB边上一点,∠BCE=16°,EF∥BC交DC于点F.
(1)依题意补全图形,并求∠FEC的度数;
(2)若∠A=141°,求∠AEC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com