
【题目】已知:二次函数y=ax2+bx+c, y与x的一些对应值如下表:
x | …… | 1 | 0 | 1 | 2 | 3 | 4 | …… |
ax2+bx+c | …… | 3 | 1 | 3 | …… |
(1)根据表格中的数据,确定二次函数解析式为_________________;
(2)填齐表格中空白处的对应值并利用上表,用五点作图法,画出二次函数y=ax2+bx+c的图象.(不必重新列表)
(3)当 1 < x ≤4时,y的取值范围是_________________;

【答案】(1) y= x2-4x+3;(2)图象见解析;(3)-1≤y≤3
【解析】(1)把表中三组对应值代入y=ax2+bx+c中得关于a、b、c的方程组,然后解方程组求出a、b、c即可得到抛物线解析式,然后计算自变量为-1、1、3所对应的函数值;
(2)先把解析式配成顶点式,然后利用描点法画函数图象,再利用函数图象写出1<x≤4时所对应y的取值范围.
(1)将点(0,3),(2,-1),(4,3)代入y=ax2+bx+c中,
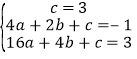 ,解得:
,解得: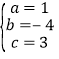 ,
,
∴二次函数解析式为![]() ,
,
当x=-1时,y=8;当x=1时,y=0;当x=3时,y=0.
(2)如图,
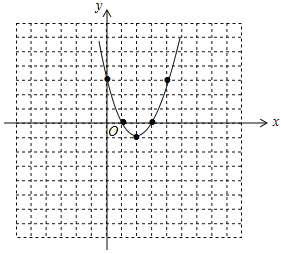
![]() ,抛物线的顶点坐标为(2,-1),
,抛物线的顶点坐标为(2,-1),
当![]() 时,y的取值范围是
时,y的取值范围是![]() .
.


科目:初中数学 来源: 题型:
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.
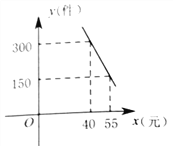
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
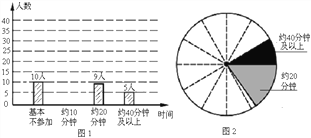
【题目】某校学生会准备调查2010级初三同学每天(除课间操外)的课外锻炼时间.
(1) 确定调查方式时,甲同学说:“我到(1)班去调查全体同学”;乙同学说:“我到体育场上去询问参加锻炼的同学”;丙同学说:“我到2010级初三每个班去随机调查一定数量的同学”.请你指出哪位同学的调查方式最为合理;
(2) 他们采用了最为合理的调查方法收集数据,并绘制出如图1所示的条形统计图和如图2所示的扇形统计图,请将条形统计图补充完整,并在扇形统计图中涂出一块表示“基本不参加”的部分;
(3) 若该校2010级初三共有240名同学,请你估计其中每天(除课间操外)课外锻炼时间不超过20分钟的人数.(注:图2中相邻两虚线形成的圆心角均为30°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算.
(1)4×(﹣![]() )÷(﹣2)
)÷(﹣2)
(2)![]()
(3)﹣1+(1﹣0.5)÷(﹣3)×[2﹣(﹣3)2]
(4)2(a2﹣ab)+3(![]() a2﹣ab)+4ab
a2﹣ab)+4ab
查看答案和解析>>
科目:初中数学 来源: 题型:
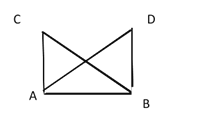
【题目】如图,海岸上有 A,B 两个观测点,点 B 在点 A 的正东方,海岛 C 在观测点 A 的正北方, 海岛 D 在观测点 B 的正北方。如果从观测点 A 看海岛 C,D 的视角∠CAD 与从观测点 B 海岛 C,D 的视角∠CBD 相等,那么海岛 C,D 到观测点 A,B 所在海岸的距离 CA,DB 相等,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点 C为线段 AB上一点,分别以 AC、BC为边在线段 AB同侧作△ACD和△BCE,且 CA=CD,CB=CE,∠ACD=∠BCE,直线 AE与 BD交于点 F
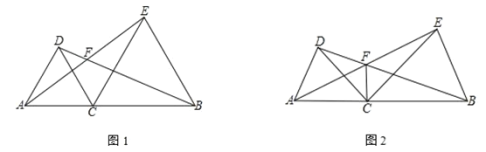
(1)如图 1,若∠ACD=60°,则∠AFD=
(2)如图 2,若∠ACD=α,连接 CF,则∠AFC= (用含α的式子表示)
(3) 将图 1 中的△ACD绕点 C顺时针旋转如图 3,连接 AE、AB、BD,∠ABD=80°,求∠EAB的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆出租车从![]() 地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下(
地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下(![]() 且
且![]() ,单位:km)
,单位:km)
第一次 | 第二次 | 第三次 | 第四次 |
|
|
| 2(9-x) |
(1)求经过连续![]() 次行驶后,这辆出租车所在的位置;
次行驶后,这辆出租车所在的位置;
(2)这辆出租车一共行驶了多少路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B、C为数轴上三点,若点C到点A的距离是点C到点B的距离的2倍,则称点C是(A,B)的奇异点,例如图1中,点A表示的数为﹣1,点B表示的数为2,表示1的点C到点A的距离为2,到点B的距离为1,则点C是(A,B)的奇异点,但不是(B,A)的奇异点.
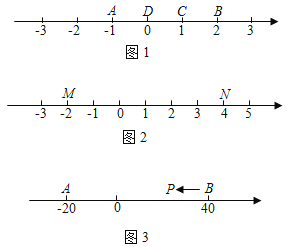
(1)在图1中,直接说出点D是(A,B)还是(B,C)的奇异点;
(2)如图2,若数轴上M、N两点表示的数分别为﹣2和4,
①若(M,N)的奇异点K在M、N两点之间,则K点表示的数是 ;
②若(M,N)的奇异点K在点N的右侧,请求出K点表示的数.
(3)如图3,A、B在数轴上表示的数分别为﹣20和40,现有一点P从点B出发,向左运动.若点P到达点A停止,则当点P表示的数为多少时,P、A、B中恰有一个点为其余两点的奇异点?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com