
【题目】如图是2019年1月份的日历.任意选择图中的菱形框部分,将每个菱形框部分中去掉中间位置的数之后,相对的两对数分别相乘,再相减,例如:9×11-3×17=48,13×15-7×21=48.不难发现,结果都是48
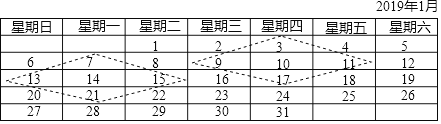
(1)请证明发现的规律;
(2)小明说:他用一个如图所示菱形框,框出5个数字,其中最小数与最大数的积是120,请判断他的说法是否正确.
【答案】(1)见解析;(2)小明的说法不正确,理由见解析
【解析】
(1)设中间的数为a,则另外4个数分别为(a-7),(a-1),(a+1),(a+7),利用相对的两对数分别相乘再相减,可证出规律成立;
(2)设这5个数中最大数为x,则最小数为(x-14),根据最小数与最大数的积是120,即可得出关于x的一元二次方程,解之取其正值,由该值在第一列可知不符合题意,进而可得出小明的说法不正确.
(1)证明:设中间的数为a,则另外4个数分别为(a-7),(a-1),(a+1),(a+7),
∴(a-1)(a+1)-(a-7)(a+7)=a2-1-(a2-49)=48.
(2)解:设这5个数中最大数为x,则最小数为(x-14),
依题意,得:x(x-14)=120,
解得:x1=20,x2=-6(不合题意,舍去).
∵20在第一列,
∴不符合题意,
∴小明的说法不正确


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完成:
(1)化简函数解析式,当![]() 时,
时,![]() ___________,当
___________,当![]() 时
时![]() ____________;
____________;
(2)根据(1)中的结果,请在所给坐标系中画出函数![]() 的图象;备用图
的图象;备用图
(3)结合画出的函数图象,解决问题:若关于![]() 的方程
的方程![]() 只有一个实数根,直接写出实数
只有一个实数根,直接写出实数![]() 的取值范围:___________________________.
的取值范围:___________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为![]() 万元/辆,经销一段时间后发现:当该型号汽车售价定为
万元/辆,经销一段时间后发现:当该型号汽车售价定为![]() 万元/辆时,平均每周售出
万元/辆时,平均每周售出![]() 辆;售价每降低
辆;售价每降低![]() 万元,平均每周多售出
万元,平均每周多售出![]() 辆.
辆.
(1)当售价为![]() 万元/辆时,平均每周的销售利润为___________万元;
万元/辆时,平均每周的销售利润为___________万元;
(2)若该店计划平均每周的销售利润是![]() 万元,为了尽快减少库存,求每辆汽车的售价.
万元,为了尽快减少库存,求每辆汽车的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回).某顾客刚好消费200元,则该顾客所获得购物券的金额超过30元的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2, AD=2![]() ,动点P从点A出发向终点D运动,连BP,并过点C作CH⊥BP,垂足为H.①△ABP∽△HCB;②AH的最小值为
,动点P从点A出发向终点D运动,连BP,并过点C作CH⊥BP,垂足为H.①△ABP∽△HCB;②AH的最小值为![]() -
-![]() ; ③在运动过程中,BP扫过的面积始终等于CH扫过的面积:④在运动过程中,点H的运动路径的长为
; ③在运动过程中,BP扫过的面积始终等于CH扫过的面积:④在运动过程中,点H的运动路径的长为![]() , 其中正确的有( )
, 其中正确的有( )
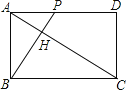
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为﹣3和1;④a﹣2b+c>0,其中正确的命题是( )
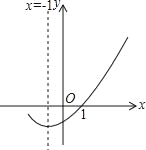
A. ①②③B. ①③C. ①④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O过正方形ABCD的顶点A、D且与边BC相切于点E,分别交AB、DC于点M、N.动点P在⊙O或正方形ABCD的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x,圆心O与P点的距离为y,图2记录了一段时间里y与x的函数关系,在这段时间里P点的运动路径为( )

A. 从D点出发,沿弧DA→弧AM→线段BM→线段BC
B. 从B点出发,沿线段BC→线段CN→弧ND→弧DA
C. 从A点出发,沿弧AM→线段BM→线段BC→线段CN
D. 从C点出发,沿线段CN→弧ND→弧DA→线段AB
查看答案和解析>>
科目:初中数学 来源: 题型:
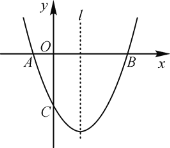
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,-3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数解析式;
(2)设点M是直线l上的一个动点,当点M到点A,点C的距离之和最短时,求点M的坐标;
(3)在抛物线上是否存在点N,使S⊿ABN=![]() S⊿ABC,若存在,求出点N的坐标,若不存在,说明理由.
S⊿ABC,若存在,求出点N的坐标,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com