
【题目】如图,矩形ABCD中,AB=2, AD=2![]() ,动点P从点A出发向终点D运动,连BP,并过点C作CH⊥BP,垂足为H.①△ABP∽△HCB;②AH的最小值为
,动点P从点A出发向终点D运动,连BP,并过点C作CH⊥BP,垂足为H.①△ABP∽△HCB;②AH的最小值为![]() -
-![]() ; ③在运动过程中,BP扫过的面积始终等于CH扫过的面积:④在运动过程中,点H的运动路径的长为
; ③在运动过程中,BP扫过的面积始终等于CH扫过的面积:④在运动过程中,点H的运动路径的长为![]() , 其中正确的有( )
, 其中正确的有( )
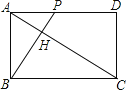
A. ①②③B. ①②④C. ②③④D. ①③④
科目:初中数学 来源: 题型:
【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,点E、F分别在菱形的边BC、CD上运动,且∠EAF=60°且E、F不与B、C、D重合,连接AC交EF于P点.
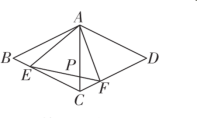
(1)证明:不论E、F在BC、CD上如何运动,总有BE=CF;
(2)当BE=1时,求AP的长;
(3)当点E、F在BC、CD上滑动时,分别探讨四边形AECF和△CEF的面积是否发生变化?如果不变,直接写出这个定值;如果变化,是最大值还是最小值?并直接写出最大(或最小)值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+ax+b经过点A(﹣2,0),B(1,3).
(1)求抛物线的解析式;
(2)由图象直接写出:x取何值时,y随x的增大而减少;
(3)根据图象回答:x取何值时,y>0.
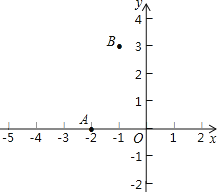
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个转盘中指针落在每个数字上的机会相等,现同时转动![]() 、
、![]() 两个转盘,停止后,指针各指向一个数字.小聪和小明利用这两个转盘做游戏:若两数之和为负数,则小聪胜;否则,小明胜.你认为这个游戏公平吗?如果不公平,对谁更有利?请你利用树状图或列表法说明理由.
两个转盘,停止后,指针各指向一个数字.小聪和小明利用这两个转盘做游戏:若两数之和为负数,则小聪胜;否则,小明胜.你认为这个游戏公平吗?如果不公平,对谁更有利?请你利用树状图或列表法说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是2019年1月份的日历.任意选择图中的菱形框部分,将每个菱形框部分中去掉中间位置的数之后,相对的两对数分别相乘,再相减,例如:9×11-3×17=48,13×15-7×21=48.不难发现,结果都是48
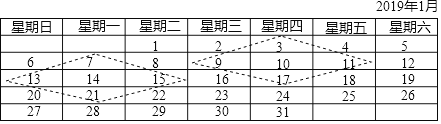
(1)请证明发现的规律;
(2)小明说:他用一个如图所示菱形框,框出5个数字,其中最小数与最大数的积是120,请判断他的说法是否正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(-1,0)、B(4,0)、C(0,2)三点.
(1)求该二次函数的解析式;
(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;
(3)点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若△PEB、△CEF的面积分别为S1、S2,求S1-S2的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象,若直线y=2x+b与这个新图象有3个公共点,则b的值为( )
A. ﹣![]() 或﹣12B. ﹣
或﹣12B. ﹣![]() 或2C. ﹣12或2D. ﹣
或2C. ﹣12或2D. ﹣![]() 或﹣12
或﹣12
查看答案和解析>>
科目:初中数学 来源: 题型:
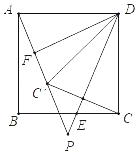
【题目】如图,在正方形ABCD中,E是边BC上的一动点(不与点B、C重合),连接DE、点C关于直线DE的对称点为C′,连接AC′并延长交直线DE于点P,F是AC′的中点,连接DF.
(1)求∠FDP的度数;
(2)连接BP,请用等式表示AP、BP、DP三条线段之间的数量关系,并证明;
(3)连接AC,若正方形的边长为![]() ,请直接写出△ACC′的面积最大值.
,请直接写出△ACC′的面积最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使AB=AC,连接AC,过点D作DE⊥AC,垂足为 E.
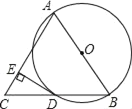
(1)求证:DC=BD;
(2)求证:DE为⊙O的切线;
(3)若AB=12,AD=6![]() ,连接OD,求扇形BOD的面积.
,连接OD,求扇形BOD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com