
【题目】已知:AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使AB=AC,连接AC,过点D作DE⊥AC,垂足为 E.
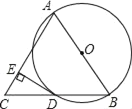
(1)求证:DC=BD;
(2)求证:DE为⊙O的切线;
(3)若AB=12,AD=6![]() ,连接OD,求扇形BOD的面积.
,连接OD,求扇形BOD的面积.
【答案】(1)见解析;(2)见解析;(3)6π
【解析】
(1)连接AD,根据圆周角定理得到∠ADB=90°,然后由三线合一可得结论;
(2)连接OD,证明OD∥AC,得到∠ODE=90°即可;
(3)根据三角函数的定义得到sinB=![]() =
=![]() =
=![]() ,求得∠B=60°,得到∠BOD=60°,根据扇形的面积公式即可得到结论.
,求得∠B=60°,得到∠BOD=60°,根据扇形的面积公式即可得到结论.
证明:(1)连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
又∵AB=AC,
∴DC=BD;
(2)连接OD,
∵OA=OB,CD=BD,
∴OD∥AC,
∴∠ODE=∠CED,
又∵DE⊥AC,
∴∠CED=90°,
∴∠ODE=90°,即OD⊥DE.
∴DE是⊙O的切线;
(3)∵AB=12,AD=6![]() ,
,
∴sinB=![]() =
=![]() =
=![]() ,
,
∴∠B=60°,
∴∠BOD=60°,
∴S扇形BOD=![]() =6π.
=6π.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2, AD=2![]() ,动点P从点A出发向终点D运动,连BP,并过点C作CH⊥BP,垂足为H.①△ABP∽△HCB;②AH的最小值为
,动点P从点A出发向终点D运动,连BP,并过点C作CH⊥BP,垂足为H.①△ABP∽△HCB;②AH的最小值为![]() -
-![]() ; ③在运动过程中,BP扫过的面积始终等于CH扫过的面积:④在运动过程中,点H的运动路径的长为
; ③在运动过程中,BP扫过的面积始终等于CH扫过的面积:④在运动过程中,点H的运动路径的长为![]() , 其中正确的有( )
, 其中正确的有( )
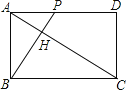
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是正方形ABCD内一点,△MBC是等边三角形,连接AM、MD.对角线BD交CM于点N,现有以下结论:①∠AMD=150°;②MA2=MNMC;③![]() ;④
;④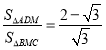 ,其中正确的结论有____(填写序号).
,其中正确的结论有____(填写序号).
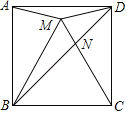
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0.
(1)当方程有一个根为﹣1时,求k的值及另一个根;
(2)当方程有两个不相等的实数根,求k的取值范围;
(3)若方程两实根x1、x2满足x1+x2=x1x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,-3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数解析式;
(2)设点M是直线l上的一个动点,当点M到点A,点C的距离之和最短时,求点M的坐标;
(3)在抛物线上是否存在点N,使S⊿ABN=![]() S⊿ABC,若存在,求出点N的坐标,若不存在,说明理由.
S⊿ABC,若存在,求出点N的坐标,若不存在,说明理由.
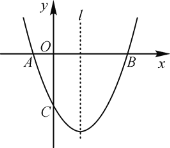
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈尔滨市滑雪业提前进入旺季,某体育用品商店购进一批简易滑雪板,每件进价为100元,售价为130元,每星期可卖出80件.商家决定降价促销,根据市场调查,每降价5元,每星期可多卖出20件.
(1)设商家每件售价x元,每星期的销售数量为y元,求y与x之间的函数关系式;
(2)降价后,商家要使每星期的销售利润W最大,应将售价定为多少元?最大销售利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在等腰![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 匀速运动,动点
匀速运动,动点![]() 同时从点
同时从点![]() 出发以同样的速度沿
出发以同样的速度沿![]() 的延长线方向匀速运动,当点
的延长线方向匀速运动,当点![]() 到达点
到达点![]() 时,点
时,点![]() 、
、![]() 同时停止运动,设运动时间为
同时停止运动,设运动时间为![]()
![]() .过点
.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为边作平行四边形
为边作平行四边形![]() .
.
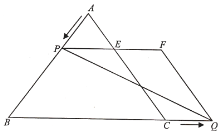
(1)当![]() 为何值时,
为何值时,![]() 为直角三角形;
为直角三角形;
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)在运动过程中,是否存在某一时刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(4)是否存在某一时刻![]() ,使点
,使点![]() 在
在![]() 的平分线上?若存在,求出
的平分线上?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() (x﹣k)2+
(x﹣k)2+![]() 经过点D(﹣1,0),与x轴正半轴交于点E,与y轴交于点C,过点C作CB∥x轴交抛物线于点B.连接BD交y轴于点F.
经过点D(﹣1,0),与x轴正半轴交于点E,与y轴交于点C,过点C作CB∥x轴交抛物线于点B.连接BD交y轴于点F.
(1)求点E的坐标.
(2)求△CFB的面积.
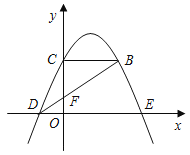
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.圆内接正六边形的边长与该圆的半径相等
B.在平面直角坐标系中,不同的坐标可以表示同一点
C.一元二次方程ax2+bx+c=0(a≠0)一定有实数根
D.将△ABC绕A点按顺时针方向旋转60°得△ADE,则△ABC与△ADE不全等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com