
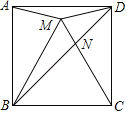
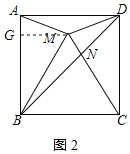
【题目】如图,点M是正方形ABCD内一点,△MBC是等边三角形,连接AM、MD.对角线BD交CM于点N,现有以下结论:①∠AMD=150°;②MA2=MNMC;③![]() ;④
;④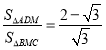 ,其中正确的结论有____(填写序号).
,其中正确的结论有____(填写序号).
【答案】①②③④.
【解析】
①先根据等边三角形得∠CMB=60°,再根据等腰三角形的性质得∠AMB=∠CMD=75°,最后根据周角的定义可得结论;
②证明△MND∽△MDC,列比例式可得结论;
③如图1,作辅助线,设NH=x,根据平行线分线段成比例定理得结论.
④如图2,设MG=x,根据直角三角形30度角的性质和勾股定理分别计算BC、AG、BG的长,根据面积公式计算可得结论;
∵△MBC是等边三角形,
∴∠MBC=∠MCB=∠CMB=60°,BM=BC,
∵四边形ABCD是正方形,
∴∠ABC=∠BCD=∠BAD=∠ADC=90°,AB=BC,
∴∠ABM=∠DCM=30°,
∵AB=BM,
∴∠AMB=∠BAM=![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
同理∠CMD=∠CDM=75°,
∴∠AMD=360°﹣75°﹣75°﹣60°=150°;
故①正确;
∵四边形ABCD是正方形,
∴∠BDC=45°,
∴∠MDN=∠CDM﹣∠BDC=75°﹣45°=30°,
∵∠CMD=∠CMD,∠MDN=∠DCM=30°,
∴△MND∽△MDC,
∴![]() =
=![]() ,
,
∴DM2=MNMC,
∵∠BAD=∠ADC,∠BAM=∠CDM,
∴∠MAD=∠MDA,
∴MA=DM,
∴MA2=MNMC,
故②正确;
过N作NH⊥CD于H,设NH=x,如图1所示:
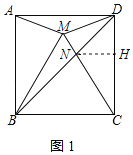
则NH⊥BC,∠NDH=∠DNH=45°,
∴NH=DH=x,
∵∠NCH=30°,∠CHN=90°
∴CN=2x,CH=![]() x,
x,
∵NH∥BC,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
故③正确;
过M作MG⊥AB于G,如图2所示:
设MG=x,
Rt△BGM中,∠GBM=30°,
∴BM=BC=AB=2x,BG=![]() x,
x,
∴AG=2x﹣![]() x,
x,
∴![]() =
=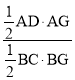 =
=![]() =
=![]() =
=![]() ,
,
故④正确;
故答案为:①②③④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+ax+b经过点A(﹣2,0),B(1,3).
(1)求抛物线的解析式;
(2)由图象直接写出:x取何值时,y随x的增大而减少;
(3)根据图象回答:x取何值时,y>0.
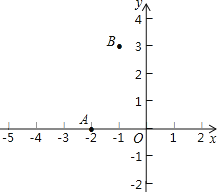
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象,若直线y=2x+b与这个新图象有3个公共点,则b的值为( )
A. ﹣![]() 或﹣12B. ﹣
或﹣12B. ﹣![]() 或2C. ﹣12或2D. ﹣
或2C. ﹣12或2D. ﹣![]() 或﹣12
或﹣12
查看答案和解析>>
科目:初中数学 来源: 题型:
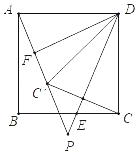
【题目】如图,在正方形ABCD中,E是边BC上的一动点(不与点B、C重合),连接DE、点C关于直线DE的对称点为C′,连接AC′并延长交直线DE于点P,F是AC′的中点,连接DF.
(1)求∠FDP的度数;
(2)连接BP,请用等式表示AP、BP、DP三条线段之间的数量关系,并证明;
(3)连接AC,若正方形的边长为![]() ,请直接写出△ACC′的面积最大值.
,请直接写出△ACC′的面积最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,点E在弦AB所对的优弧上,且![]() 为半圆,C是
为半圆,C是![]() 上的动点,连接CA、CB,已知AB=4cm,设B、C间的距离为xcm,点C到弦AB所在直线的距离为y1cm,A、C两点间的距离为y2cm.
上的动点,连接CA、CB,已知AB=4cm,设B、C间的距离为xcm,点C到弦AB所在直线的距离为y1cm,A、C两点间的距离为y2cm.
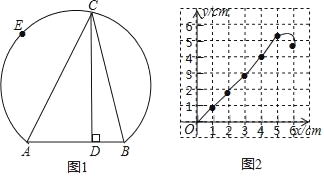
小明根据学习函数的经验,分别对函数y1、y2岁自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整.
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1、y2与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 0.78 | 1.76 | 2.85 | 3.98 | 4.95 | 4.47 |
y2/cm | 4 | 4.69 | 5.26 | 5.96 | 5.94 | 4.47 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1、y2的图象;
(3)结合函数图象,解决问题:
①连接BE,则BE的长约为 cm.
②当以A、B、C为顶点组成的三角形是直角三角形时,BC的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,现给出以下四个结论:(1)AE=CF;(2)△EPF是等腰直角三角形;(3)S四边形AEPF=![]() S△ABC;(4)当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP.(点E不与A、B重合),上述结论中是正确的结论的概率是( )
S△ABC;(4)当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP.(点E不与A、B重合),上述结论中是正确的结论的概率是( )

A.1个B.3个C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
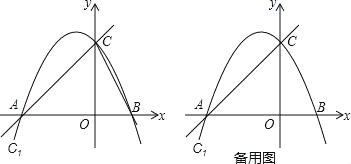
【题目】如图,抛物线![]() 与x轴交于A(﹣4,0)、B(2,0)两点,与y轴交于C,M为此抛物线的顶点.
与x轴交于A(﹣4,0)、B(2,0)两点,与y轴交于C,M为此抛物线的顶点.
(1)求此抛物线的函数解析式;
(2)动直线l从与直线AC重合的位置出发,绕点A顺时针旋转,与直线AB重合时终止运动,直线l与BC交于点D,P是线段AD的中点.
①直接写出点P所经过的路线长为 ;
②点D与B、C不重合时,过点D作DE⊥AC于点E,作DF⊥AB于点F,连接PE、PF、EF,在旋转过程中,求EF的最小值;
(3)将抛物线C1平移得到抛物线C2,已知抛物线C2的顶点为N,与直线AC交于E、F两点,若EF=AC,求直线MN的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使AB=AC,连接AC,过点D作DE⊥AC,垂足为 E.
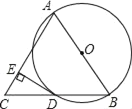
(1)求证:DC=BD;
(2)求证:DE为⊙O的切线;
(3)若AB=12,AD=6![]() ,连接OD,求扇形BOD的面积.
,连接OD,求扇形BOD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
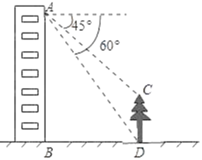
【题目】如图,小明在教学楼的窗户A处,测量楼前的一棵树CD的高.现测得树顶C处的俯角为45°,树底D处的俯角为60°,楼底到大树的距离BD为10米.请你帮助小明计算树的高度(精确到0.1米).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com