练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】将二次函数y＝x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新图象，若直线y＝2x+b与这个新图象有3个公共点，则b的值为（　　）

    A. ﹣或﹣12B. ﹣或2C. ﹣12或2D. ﹣或﹣12

    【答案】A

    【解析】

    如图所示，过点B作直线y=2x+b，将直线向下平移到恰在点C处相切，则一次函数y=2x+b在这两个位置时，两个图象有3个交点，即可求解．

    如图所示，过点B的直线y＝2x+b与新抛物线有三个公共点，将直线向下平移到恰在点C处相切，此时与新抛物线也有三个公共点，

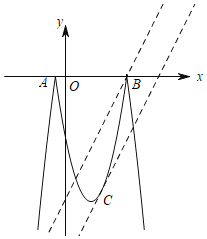
    令y＝x2﹣5x﹣6＝0，解得：x＝﹣1或6，即点B坐标（6，0），

    将一次函数与二次函数表达式联立得：x2﹣5x﹣6＝2x+b，整理得：x2﹣7x﹣6﹣b＝0，

    △＝49+4（﹣6﹣b）＝0，解得：b＝﹣，

    当一次函数过点B时，将点B坐标代入：y＝2x+b得：0＝12+b，解得：b＝﹣12，

    综上，直线y＝2x+b与这个新图象有3个公共点，则b的值为﹣12或﹣；

    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料：

    已知实数m，n满足(2m2＋n2＋1)(2m2＋n2－1)＝80，试求2m2＋n2的值.

    解：设2m2＋n2＝t，则原方程变为(t＋1)(t－1)＝80，整理得t2－1＝80，t2＝81，

    所以t＝土9，因为2m2＋n2＞0，所以2m2＋n2＝9.

    上面这种方法称为“换元法”，把其中某些部分看成一个整休，并用新字母代替(即换元)，则能使复杂的问题简单化.

    根据以上阅读材料内容，解决下列问题，并写出解答过程.

    （1）已知实数x、y，满足(2x2＋2y2＋3)(2x2＋2y2－3)＝27，求x2＋y2的值.

    （2）已知Rt△ACB的三边为a、b、c（c为斜边），其中a、b满足(a2＋b2)(a2＋b2－4)＝5，求Rt△ACB外接圆的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在四边形ABCD中,∠B+∠D=180°,对角线AC平分∠BAD

    (1)如图1,若∠DAB=120°,且∠B=90°,易证AD+BA＝AC

    (2)如图2,若将(1)中的条件“∠B=90°”去掉,(1)中的结论是否成立?请说明理由.

    (3)如图3,若∠DAB=90°,探究边AD、AB与对角线AC的数量关系并说明理由.

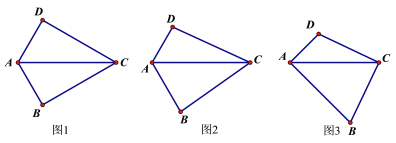
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，抛物线y＝ax2+bx+3与坐标轴分别交于点A，B（﹣3，0），C（1，0），点P是线段AB上方抛物线上的一个动点．

    （1）求抛物线解析式；

    （2）当点P运动到什么位置时，△PAB的面积最大？

    （3）过点P作x轴的垂线，交线段AB于点D，再过点P作PE∥x轴交抛物线于点E，连接DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求点P的坐标；若不存在，说明理由．

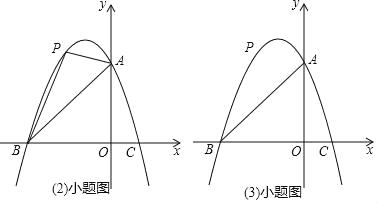
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=x2-（2m+1）x-3m．
    （1）若m=2，则该函数的表达式为_____，求出函数图象的对称轴为_____．
    （2）对于此函数，在-1≤x≤1的范围内至少有x值使得y≥0，则m的取值范围为____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某蔬菜种植基地为提高蔬菜产量，计划对甲、乙两种型号蔬菜大棚进行改造，根据预算，改造2个甲种型号大棚比1个乙种型号大棚多需资金6万元，改造1个甲种型号大棚和2个乙种型号大棚共需资金48万元．

    （1）改造1个甲种型号和1个乙种型号大棚所需资金分别是多少万元？

    （2）已知改造1个甲种型号大棚的时间是5天，改造1个乙种型号大概的时间是3天，该基地计划改造甲、乙两种蔬菜大棚共8个，改造资金最多能投入128万元，要求改造时间不超过35天，请问有几种改造方案？哪种方案基地投入资金最少，最少是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

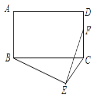
    【题目】如图，在矩形ABCD中，AB=6，AD=8，以BC为斜边在矩形所在平面作直角三角形BEC，F为CD的中点，则EF的最小值为 （ ）

    A. B. 4C. D. 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

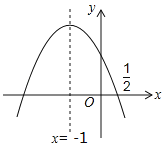
    【题目】（4分）如图，抛物线的对称轴是．且过点（，0），有下列结论：①abc＞0；②a﹣2b+4c=0；③25a﹣10b+4c=0；④3b+2c＞0；⑤a﹣b≥m（am﹣b）；其中所有正确的结论是 ．（填写正确结论的序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.

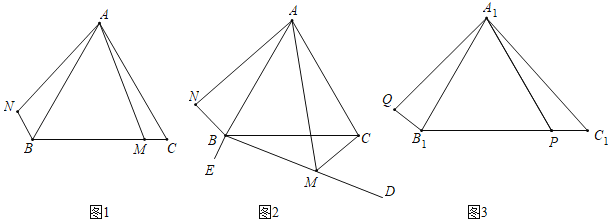
    （一）猜测探究

    在中，，是平面内任意一点，将线段绕点按顺时针方向旋转与相等的角度，得到线段，连接．

    （1）如图1，若是线段上的任意一点，请直接写出与的数量关系是　 　，与的数量关系是　 　；

    （2）如图2，点是延长线上点，若是内部射线上任意一点，连接，（1）中结论是否仍然成立？若成立，请给予证明，若不成立，请说明理由．

    （二）拓展应用

    如图3，在中，，，，是上的任意点，连接，将绕点按顺时针方向旋转，得到线段，连接．求线段长度的最小值．

    查看答案和解析>>

    同步练习册答案