
【题目】已知二次函数y=x2-(2m+1)x-3m.
(1)若m=2,则该函数的表达式为_____,求出函数图象的对称轴为_____.
(2)对于此函数,在-1≤x≤1的范围内至少有x值使得y≥0,则m的取值范围为____.
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线C1:y=(x+![]() )2,平移抛物线y=﹣x2,使其顶点D在抛物线C1位于y轴右侧的图象上,得到抛物线C2,抛物线C2交x轴于A、B两点(点A在点B的左侧),交y轴于点C,设点D的横坐标为a.
)2,平移抛物线y=﹣x2,使其顶点D在抛物线C1位于y轴右侧的图象上,得到抛物线C2,抛物线C2交x轴于A、B两点(点A在点B的左侧),交y轴于点C,设点D的横坐标为a.

(1)当OC=2时,求抛物线C2的解析式;
(2)在抛物线的C2的对称轴上是否存在一点P,使得AP+CP的长最短?若存在,求出点P的坐标(用含a的代数式表示);若不存在,请说明理由;
(3)在(2)的条件下,连接OP,若OP⊥BC,求此时a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
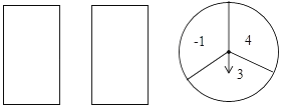
【题目】小红玩抽卡片和旋转盘游戏,有两张正面分别标有数字1,﹣2的不透明卡片,背面完全相同;转盘被平均分成3个相等的扇形,并分别标有数字﹣1,3,4(如图所示),小云把卡片背面朝上洗匀后从中随机抽出一张,记下卡片上的数字;然后转动转盘,转盘停止后,记下指针所在区域的数字(若指针在分格线上,则重转一次,直到指针指向某一区域为止).请用列表或树状图的方法(只选其中一种)求出两个数字之积为负数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)如图,直线y=x+m和抛物线y=![]() +bx+c都经过点A(1,0),
+bx+c都经过点A(1,0),
B(3,2).

(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
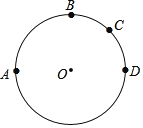
【题目】如图所示A、B、C、D四点在⊙O上的位置,其中![]() =180°,且
=180°,且![]() =
=![]() ,
,![]() =
=![]() .若阿超在
.若阿超在![]() 上取一点P,在
上取一点P,在![]() 上取一点Q,使得∠APQ=130°,则下列叙述何者正确( )
上取一点Q,使得∠APQ=130°,则下列叙述何者正确( )
A. Q点在![]() 上,且
上,且![]() >
>![]() B. Q点在
B. Q点在![]() 上,且
上,且![]() <
<![]()
C. Q点在![]() 上,且
上,且![]() >
>![]() D. Q点在
D. Q点在![]() 上,且
上,且![]() <
<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象,若直线y=2x+b与这个新图象有3个公共点,则b的值为( )
A. ﹣![]() 或﹣12B. ﹣
或﹣12B. ﹣![]() 或2C. ﹣12或2D. ﹣
或2C. ﹣12或2D. ﹣![]() 或﹣12
或﹣12
查看答案和解析>>
科目:初中数学 来源: 题型:
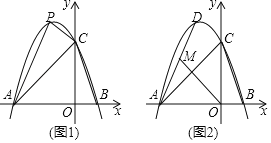
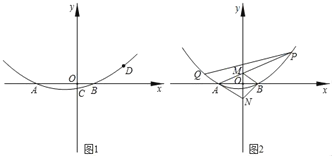
【题目】如图,抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点.
(1)求抛物线的函数表达式;
(2)如图1,P为抛物线上在第二象限内的一点,若△PAC面积为3,求点P的坐标;
(3)如图2,D为抛物线的顶点,在线段AD上是否存在点M,使得以M,A,O为顶点的三角形与△ABC相似?若存在,求点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠DAF=300,M是CD上一点,AM的延长线交BC的延长线于点F,BE垂直平分AM,DG∥AF,MG∥DE.
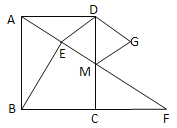
(1)判断四边形DEMG的形状,并说明理由;
(2)求证:△ADM≌△FCM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣2a与x轴交于点A和点B(1,0),与y轴将于点C(0,﹣![]() ).
).
(1)求抛物线的解析式;
(2)若点D(2,n)是抛物线上的一点,在y轴左侧的抛物线上存在点T,使△TAD的面积等于△TBD的面积,求出所有满足条件的点T的坐标;
(3)直线y=kx﹣k+2,与抛物线交于两点P、Q,其中在点P在第一象限,点Q在第二象限,PA交y轴于点M,QA交y轴于点N,连接BM、BN,试判断△BMN的形状并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com