
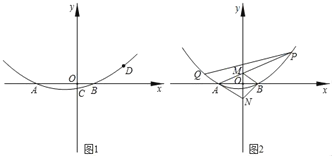
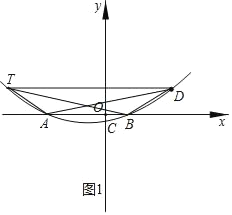
【题目】如图,抛物线y=ax2+bx﹣2a与x轴交于点A和点B(1,0),与y轴将于点C(0,﹣![]() ).
).
(1)求抛物线的解析式;
(2)若点D(2,n)是抛物线上的一点,在y轴左侧的抛物线上存在点T,使△TAD的面积等于△TBD的面积,求出所有满足条件的点T的坐标;
(3)直线y=kx﹣k+2,与抛物线交于两点P、Q,其中在点P在第一象限,点Q在第二象限,PA交y轴于点M,QA交y轴于点N,连接BM、BN,试判断△BMN的形状并证明你的结论.
【答案】(1)![]() ;(2)(﹣3,
;(2)(﹣3,![]() )与(﹣
)与(﹣![]() ,﹣
,﹣![]() ;(3)△BMN是直角三角形,证明见解析.
;(3)△BMN是直角三角形,证明见解析.
【解析】
(1)用待定系数法即能求出抛物线的解析式;
(2)△TAD与△TBD有公共底边TD,面积相等即点A.点B到直线TD距离相等。根据T的位置关系分类讨论:在点A左侧时,根据“平行线间距离处处相等”可得AB∥TD,易得点T的纵坐标,代入解析式即求出横坐标;在点A右侧时,分别过A.B作TD的垂线段,构造全等三角形,证得TD与x轴交点为AB中点,求出TD解析式,再与抛物线解析式联立方程组求出T;
(3)联立直线y=kxk+2与抛物线解析式,整理得关于x的一元二次方程,根据韦达定理得到P、Q横坐标和和与积的式子(用k表示).设M(0,m)、N(0,n),求出直线AP、AQ的解析式(分别用m、n表示).分别联立直线AP、AQ与抛物线方程,求得P、Q的横坐标(分别用m、n表示),即得到关于m、n、k关系的式子,整理得mn=1,即OMON=1,易证△BOM∽△NOB,进而求出∠MBN=90°.
解:(1)∵抛物线y=ax2+bx﹣2a经过点B(1,0)、C(0,![]() )
)
∴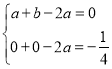
解得:![]()
∴抛物线的解析式为:![]() .
.
(2)当x=2时,n=![]() ×22+
×22+![]() ×2
×2![]() =
=![]()
∴D(2,![]() )
)
①当点T在点A左侧时,如图1,
∵S△TAD=S△TBD,且△TAD与△TBD有公共底边为TD
∴AB∥TD,即TD∥x轴
∴yT=yD=![]()
![]() x2+
x2+![]() x
x![]() =
=![]() 解得:x1=﹣3,x2=2(即点D横坐标,舍去)
解得:x1=﹣3,x2=2(即点D横坐标,舍去)
∴T(﹣3,![]() )
)
②当点T在点A右侧时,如图2,设DT与x轴交点为P,过A作AE⊥DT于E,过B作BF⊥DT于F
∵S△TAD=S△TBD,且△TAD与△TBD有公共底边为TD
∴AE=BF
在△AEP与△BFP中,
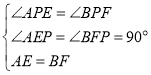
∴△AEP≌△BFP(AAS)
∴AP=BP 即P为AB中点
由![]() x2+
x2+![]() x
x![]() =0 解得:x1=﹣2,x2=1
=0 解得:x1=﹣2,x2=1
∴A(﹣2,0)
∴P(![]() ,0)
,0)
设直线DP:y=kx+c
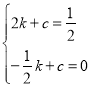
解得: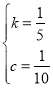
∴直线DT:y=![]()
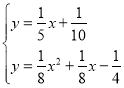
解得: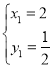 (即点D,舍去),
(即点D,舍去),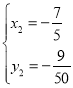
∴T(﹣![]() ,﹣
,﹣![]() )
)
综上所述,满足条件的点T的坐标为(﹣3,![]() )与(﹣
)与(﹣![]() ,﹣
,﹣![]() )
)

(3)△BMN是直角三角形,证明如下:
设x1为点P横坐标,x2为点Q的横坐标
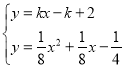 整理得:x2+(1﹣8k)x+8k﹣18=0
整理得:x2+(1﹣8k)x+8k﹣18=0
∴x1+x2=8k﹣1,x1x2=8k﹣18
设M(0,m),N(0,n)则OM=m,ON=﹣n
∴直线AM解析式:y=![]() ,直线AN解析式:y=
,直线AN解析式:y=![]()
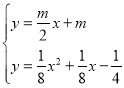
解得: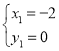 (舍去),
(舍去),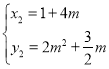
∴P(1+4m,2m2+![]() m)
m)
同理可得:Q(1+4n,2n2+![]() n)
n)
∴![]()
整理得:mn=﹣1
∴m|n|=1 即OMON=1
又OB=1,即OMON=OB2
∴![]()
∴△BOM∽△NOB
∴∠OBM=∠ONB
∴∠MBN=∠OBM+∠OBN=∠ONB+∠OBN=90°
∴△BMN是直角三角形


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-(2m+1)x-3m.
(1)若m=2,则该函数的表达式为_____,求出函数图象的对称轴为_____.
(2)对于此函数,在-1≤x≤1的范围内至少有x值使得y≥0,则m的取值范围为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
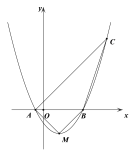
【题目】如图,已知抛物线![]() 经过点
经过点![]() 、
、![]() .
.
(1)求抛物线的解析式,并写出顶点![]() 的坐标;
的坐标;
(2)若点![]() 在抛物线上,且点
在抛物线上,且点![]() 的横坐标为8,求四边形
的横坐标为8,求四边形![]() 的面积
的面积
(3)定点![]() 在
在![]() 轴上,若将抛物线的图象向左平移2各单位,再向上平移3个单位得到一条新的抛物线,点
轴上,若将抛物线的图象向左平移2各单位,再向上平移3个单位得到一条新的抛物线,点![]() 在新的抛物线上运动,求定点
在新的抛物线上运动,求定点![]() 与动点
与动点![]() 之间距离的最小值
之间距离的最小值![]() (用含
(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
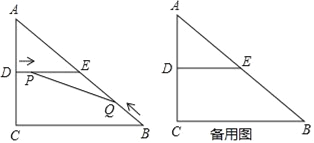
【题目】如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,D、E分别是AC、AB的中点,连接DE.点P从点D出发,沿DE方向匀速运动,速度为1cm/s;同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s.解答下列问题:
(1)当t为何值时,以点E、P、Q为顶点的三角形与△ADE相似?
(2)当t为何值时,△EPQ为等腰三角形?(直接写出答案即可);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年平昌冬奥会在2月9日到25日在韩国平昌郡举行,为了调查中学生对冬奥会比赛项目的了解程度,某中学在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解B、比较了解C、基本了解D、不了解.根据调查统计结果,绘制了如图所示的不完整的三种统计图表.
对冬奥会了解程度的统计表
对冬奥会的了解程度 | 百分比 |
A非常了解 | 10% |
B比较了解 | 15% |
C基本了解 | 35% |
D不了解 | n% |
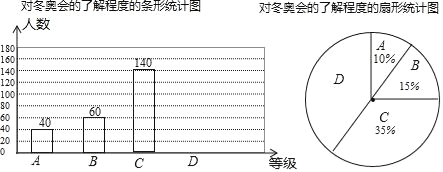
(1)n= ;
(2)扇形统计图中,D部分扇形所对应的圆心角是 ;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展冬奥会的知识竞赛,某班要从“非常了解”程度的小明和小刚中选一人参加,现设计了如下游戏来确定谁参赛,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4然后放到一个不透明的袋中,一个人先从袋中摸出一个球,另一人再从剩下的三个球中随机摸出一个球,若摸出的两个球上的数字和为偶数,则小明去,否则小刚去,请用画树状图或列表的方法说明这个游戏是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.
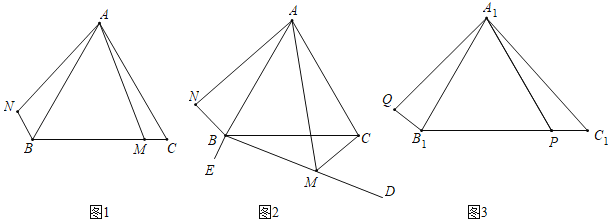
(一)猜测探究
在![]() 中,
中,![]() ,
,![]() 是平面内任意一点,将线段
是平面内任意一点,将线段![]() 绕点
绕点![]() 按顺时针方向旋转与
按顺时针方向旋转与![]() 相等的角度,得到线段
相等的角度,得到线段![]() ,连接
,连接![]() .
.
(1)如图1,若![]() 是线段
是线段![]() 上的任意一点,请直接写出
上的任意一点,请直接写出![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() 与
与![]() 的数量关系是 ;
的数量关系是 ;
(2)如图2,点![]() 是
是![]() 延长线上点,若
延长线上点,若![]() 是
是![]() 内部射线
内部射线![]() 上任意一点,连接
上任意一点,连接![]() ,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.
,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.
(二)拓展应用
如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的任意点,连接
上的任意点,连接![]() ,将
,将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() .求线段
.求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=![]() ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH=![]() ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH=![]() ,其中正确结论为( )
,其中正确结论为( )
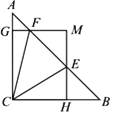
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与直线
与直线![]() 分别相交于
分别相交于![]() ,
,![]() 两点,且此抛物线与
两点,且此抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ,连接
,连接![]() ,
,![]() .已知
.已知![]() ,
,![]() .
.
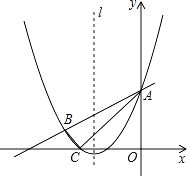
(1)求抛物线的解析式;
(2)在抛物线对称轴![]() 上找一点
上找一点![]() ,使
,使![]() 的值最大,并求出这个最大值;
的值最大,并求出这个最大值;
(3)点![]() 为
为![]() 轴右侧抛物线上一动点,连接
轴右侧抛物线上一动点,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,问:是否存在点
,问:是否存在点![]() 使得以
使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出所有符合条件的点
相似?若存在,请求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.

(1)写出图中一对全等三角形和一对相似比不为1的相似三角形;
(2)选择(1)中一对加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com