
【题目】如图,抛物线![]() 与直线
与直线![]() 分别相交于
分别相交于![]() ,
,![]() 两点,且此抛物线与
两点,且此抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ,连接
,连接![]() ,
,![]() .已知
.已知![]() ,
,![]() .
.
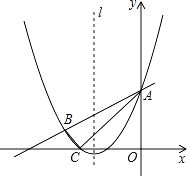
(1)求抛物线的解析式;
(2)在抛物线对称轴![]() 上找一点
上找一点![]() ,使
,使![]() 的值最大,并求出这个最大值;
的值最大,并求出这个最大值;
(3)点![]() 为
为![]() 轴右侧抛物线上一动点,连接
轴右侧抛物线上一动点,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,问:是否存在点
,问:是否存在点![]() 使得以
使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出所有符合条件的点
相似?若存在,请求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)点M的坐标为(
;(2)点M的坐标为(![]() ,
,![]() )时,
)时,![]() 取最大值为
取最大值为![]() ;(3)存在点
;(3)存在点![]() .
.
【解析】
(1)根据待定系数法求解即可;
(2)根据三角形的三边关系可知:当点![]() 、
、![]() 、
、![]() 三点共线时,可使
三点共线时,可使![]() 的值最大,据此求解即可;
的值最大,据此求解即可;
(3)先求得![]() ,再过点
,再过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,如图,这样就把以
,如图,这样就把以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似问题转化为以
相似问题转化为以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似的问题,再分当
相似的问题,再分当![]() 时与
时与![]() 时两种情况,分别求解即可.
时两种情况,分别求解即可.
解:(1)将![]() ,
,![]() 代入
代入![]() 得:
得:
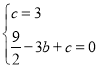 ,解得:
,解得:![]() ,
,
∴抛物线的解析式是![]() ;
;
(2)解方程组: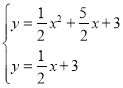 ,得
,得![]() ,
, ,
,
∵![]() ,∴
,∴![]()
当点![]() 、
、![]() 、
、![]() 三点不共线时,根据三角形三边关系得
三点不共线时,根据三角形三边关系得![]() ,
,
当点![]() 、
、![]() 、
、![]() 三点共线时,
三点共线时,![]() ,
,
∴当点![]() 、
、![]() 、
、![]() 三点共线时,
三点共线时,![]() 取最大值,即为
取最大值,即为![]() 的长,
的长,
如图,过点![]() 作BE⊥x轴于点
作BE⊥x轴于点![]() ,则在
,则在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,∴
,∴![]() 取最大值为
取最大值为![]() ;
;
易求得直线BC的解析式为:y=-x-3,抛物线的对称轴是直线![]() ,当
,当![]() 时,
时,![]() ,∴点M的坐标为(
,∴点M的坐标为(![]() ,
,![]() );
);
∴点M的坐标为(![]() ,
,![]() )时,
)时,![]() 取最大值为
取最大值为![]() ;
;
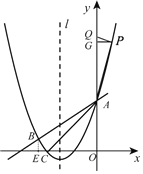
(3)存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.
设点![]() 坐标为
坐标为![]() ,
,
在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,
,
在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,如图,
,如图,
∵![]() ,
,![]() ,∴
,∴![]() ∽
∽![]() ,
,
∵![]() ,
,
∴①当![]() 时,
时,![]() ∽
∽![]() ,
,
∴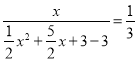 ,解得
,解得![]() ,
,![]() ,(舍去)
,(舍去)
∴点![]() 的纵坐标为
的纵坐标为![]() ,∴点
,∴点![]() 为
为![]() ;
;
②当![]() 时,
时,![]() ∽
∽![]() ,
,
∴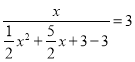 ,解得
,解得![]() (舍去),
(舍去),![]() (舍去),
(舍去),
∴此时无符合条件的点![]() ;
;
综上所述,存在点![]() .
.


科目:初中数学 来源: 题型:
【题目】材料阅读:
类比是数学中常用的数学思想.比如,我们可以类比多位数的加、减、乘、除的竖式运算方法,得到多项式与多项式的加、减、乘、除的运算方法.

理解应用:
(1)请仿照上面的竖式方法计算:![]() ;
;
(2)已知两个多项式的和为![]() ,其中一个多项式为
,其中一个多项式为![]() .请用竖式的方法求出另一个多项式.
.请用竖式的方法求出另一个多项式.
(3)已知一个长为![]() ,宽为
,宽为![]() 的矩形
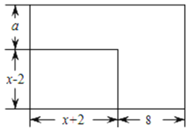
的矩形![]() ,将它的长增加8.宽增加
,将它的长增加8.宽增加![]() 得到一个新矩形
得到一个新矩形![]() ,且矩形
,且矩形![]() 的周长是
的周长是![]() 周长的3倍(如图).同时,矩形
周长的3倍(如图).同时,矩形![]() 的面积和另一个一边长为
的面积和另一个一边长为![]() 的矩形
的矩形![]() 的面积相等,求
的面积相等,求![]() 的值和矩形
的值和矩形![]() 的另一边长.
的另一边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F.
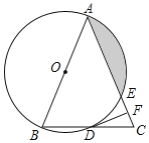
(1)求证:直线DF是⊙O的切线;
(2)求证:BC2=4CFAC;
(3)若⊙O的半径为4,∠CDF=15°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“停课不停学”期间,小明用电脑在线上课,图1是他的电脑液晶显示器的侧面图,显示屏AB可以绕O点旋转一定角度.研究表明:当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个18°俯角(即望向屏幕中心P的的视线EP与水平线EA的夹角∠AEP)时,对保护眼睛比较好,而且显示屏顶端A与底座C的连线AC与水平线CD垂直时(如图2)时,观看屏幕最舒适,此时测得∠BCD=30°,∠APE=90°,液晶显示屏的宽AB为32cm.
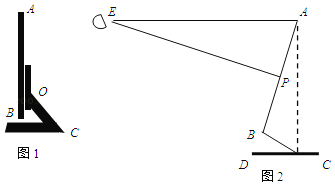
(1)求眼睛E与显示屏顶端A的水平距离AE;(结果精确到1cm)
(2)求显示屏顶端A与底座C的距离AC.(结果精确到1cm)(参考数据:sin18°≈0.3,cos18°≈0.9,tan18°≈0.3,![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
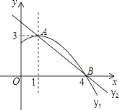
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论: ①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1 ,
其中正确的是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距![]() 一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是
一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是![]() 以快车开始行驶计时,设时间为
以快车开始行驶计时,设时间为![]() , 两车之间的距离为
, 两车之间的距离为![]() ,图中的折线是
,图中的折线是![]() 与
与![]() 的函数关系的部分图象,根据图象解决以下问题:
的函数关系的部分图象,根据图象解决以下问题:

(1)慢车的速度是_ _![]() ,点
,点![]() 的坐标是_ _;
的坐标是_ _;
(2)线段![]() 所表示的
所表示的![]() 与
与![]() 之间的函数关系式是_ ;
之间的函数关系式是_ ;
(3)试在图中补全点![]() 以后的图象.
以后的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知网格的小正方形的边长均为1,格点三角形ABC如图所示,请用没有刻度的直尺画出满足条件的图形
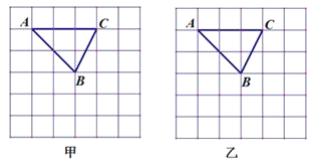
(1)在甲图中,画出△![]() ,且相似比为2:1,各顶点都在格点上.
,且相似比为2:1,各顶点都在格点上.
(2)在乙图中,把线段AB三等分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为 1寸,锯道AB=1尺(1尺=10寸),则该圆材的直径为( )
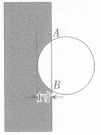
A.13B.24C.26D.28
查看答案和解析>>
科目:初中数学 来源: 题型:
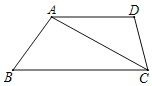
【题目】如图,在四边形ABCD中,AD∥BC.
(1)求作直线EF使得EF交AD于点E,交BC于点F且使得EA=EC,FA=FC(尺规作图,保留作图痕迹,不写作法);
(2)连接AF、CE,判断四边形AFCE的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com