
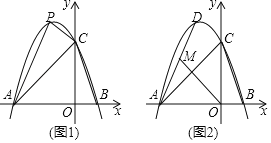
【题目】如图,抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点.
(1)求抛物线的函数表达式;
(2)如图1,P为抛物线上在第二象限内的一点,若△PAC面积为3,求点P的坐标;
(3)如图2,D为抛物线的顶点,在线段AD上是否存在点M,使得以M,A,O为顶点的三角形与△ABC相似?若存在,求点M的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2﹣2x+3;(2)点P的坐标为(﹣1,4)或(﹣2,3);(3)存在,(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),见解析.
),见解析.
【解析】
(1)利用待定系数法,然后将A、B、C的坐标代入解析式即可求得二次函数的解析式;
(2))过P点作PQ垂直x轴,交AC于Q,把△APC分成两个△APQ与△CPQ,把PQ作为两个三角形的底,通过点A,C的横坐标表示出两个三角形的高即可求得三角形的面积.
(3)通过三角形函数计算可得∠DAO=∠ACB,使得以M,A,O为顶点的三角形与△ABC相似,则有两种情况,∠AOM=∠CAB=45°,即OM为y=-x,若∠AOM=∠CBA,则OM为y=-3x+3,然后由直线解析式可求OM与AD的交点M.
(1)把A(﹣3,0),B(1,0),C(0,3)代入抛物线解析式y=ax2+bx+c得
 ,
,
解得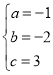 ,
,
所以抛物线的函数表达式为y=﹣x2﹣2x+3.
(2)如解(2)图1,过P点作PQ平行y轴,交AC于Q点,
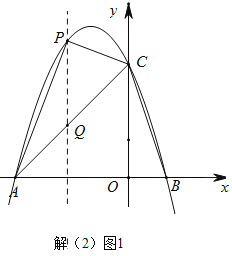
∵A(﹣3,0),C(0,3),
∴直线AC解析式为y=x+3,
设P点坐标为(x,﹣x2﹣2x+3.),则Q点坐标为(x,x+3),
∴PQ=﹣x2﹣2x+3﹣(x+3)=﹣x2﹣3x.
∴S△PAC=![]() ,
,
∴![]() ,
,
解得:x1=﹣1,x2=﹣2.
当x=﹣1时,P点坐标为(﹣1,4),
当x=﹣2时,P点坐标为(﹣2,3),
综上所述:若△PAC面积为3,点P的坐标为(﹣1,4)或(﹣2,3),
(3)如解(3)图1,过D点作DF垂直x轴于F点,过A点作AE垂直BC于E点,
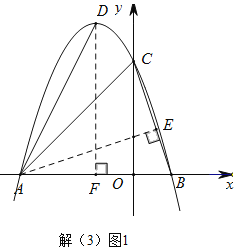
∵D为抛物线y=﹣x2﹣2x+3的顶点,
∴D点坐标为(﹣1,4),
又∵A(﹣3,0),
∴直线AC为y=2x+4,AF=2,DF=4,tan∠PAB=2,
∵B(1,0),C(0,3)
∴tan∠ABC=3,BC=![]() ,sin∠ABC=
,sin∠ABC=![]() ,直线BC解析式为y=﹣3x+3.
,直线BC解析式为y=﹣3x+3.
∵AC=4,
∴AE=ACsin∠ABC=![]() =
=![]() ,BE=
,BE=![]() ,
,
∴CE=![]() ,
,
∴tan∠ACB=![]() ,
,
∴tan∠ACB=tan∠PAB=2,
∴∠ACB=∠PAB,
∴使得以M,A,O为顶点的三角形与△ABC相似,则有两种情况,如解(3)图2
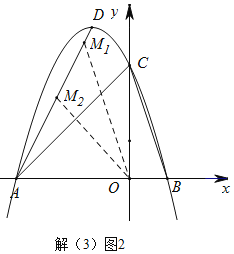
Ⅰ.当∠AOM=∠CAB=45°时,△ABC∽△OMA,
即OM为y=﹣x,
设OM与AD的交点M(x,y)
依题意得:![]() ,
,
解得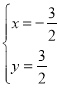 ,
,
即M点为(![]() ,
,![]() ).
).
Ⅱ.若∠AOM=∠CBA,即OM∥BC,
∵直线BC解析式为y=﹣3x+3.
∴直线OM为y=﹣3x,设直线OM与AD的交点M(x,y).则
依题意得:![]() ,
,
解得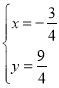 ,
,
即M点为(![]() ,
,![]() ),
),
综上所述:存在使得以M,A,O为顶点的三角形与△ABC相似的点M,其坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
【题目】2017年中秋节来期间,某超市以每盒80元的价格购进了1000盒月饼,第一周以每盒168元的价格销售了300盒,第二周如果单价不变,预计仍可售出300盒,该超市经理为了增加销量,决定降价,据调查,单价每降低1元,可多售出10盒,但最低每盒要赢利30元,第二周结束后,该超市将对剩余的月饼一次性赔钱甩卖,此时价格为70元/盒.
(1)若设第二周单价降低x元,则第二周的单价是 ______ ,销量是 ______ ;
(2)经两周后还剩余月饼 ______ 盒;
(3)若该超市想通过销售这批月饼获利51360元,那么第二周的单价应是多元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】良好的饮食对学生的身体、智力发育和健康起到了极其重要的作用,荤菜中蛋白质、钙、磷及脂溶性维生素优于素食,而素食中不饱和脂肪酸、维生素和纤维素又优于荤食,只有荤食与素食适当搭配,才能强化初中生的身体素质.某校为了了解学生的体质健康状况,以便食堂为学生提供合理膳食,对本校七年级、八年级学生的体质健康状况进行了调查,过程如下:
收集数据:从七、八年级两个年级中各抽取15名学生,进行了体质健康测试,测试成绩(百分制)如下:
七年级:74 81 75 76 70 75 75 79 81 70 74 80 91 69 82
八年级:81 94 83 77 83 80 81 70 81 73 78 82 80 70 50
整理数据:
年级 | x<60 | 60≤x<80 | 80≤x<90 | 90≤x≤100 |
七年级 | 0 | 10 | 4 | 1 |
八年级 | 1 | 5 | 8 | 1 |
(说明:90分及以上为优秀,80~90分(不含90分)为良好,60~80分(不含80分)为及格,60分以下为不及格)
分析数据:
年级 | 平均数 | 中位数 | 众数 |
七年级 |
| 75 | 75 |
八年级 | 77.5 | 80 |
|
得出结论:
(2)可以推断出 年级学生的体质健康状况更好一些,并说明理由;
(3)若七年级共有300名学生,请估计七年级体质健康成绩优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-(2m+1)x-3m.
(1)若m=2,则该函数的表达式为_____,求出函数图象的对称轴为_____.
(2)对于此函数,在-1≤x≤1的范围内至少有x值使得y≥0,则m的取值范围为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
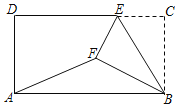
【题目】如图,在矩形ABCD中,AB=4,BC=![]() ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=
,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=![]() ,则CE=_____.
,则CE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
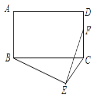
【题目】如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形所在平面作直角三角形BEC,F为CD的中点,则EF的最小值为 ( )
A. ![]() B. 4C.
B. 4C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
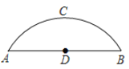
【题目】如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m.
(1)求拱桥的半径;
(2)有一艘宽为5m的货船,船舱顶部为长方形,并高出水面3.4m,则此货船是否能顺利通过此圆弧形拱桥,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
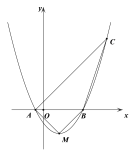
【题目】如图,已知抛物线![]() 经过点
经过点![]() 、
、![]() .
.
(1)求抛物线的解析式,并写出顶点![]() 的坐标;
的坐标;
(2)若点![]() 在抛物线上,且点
在抛物线上,且点![]() 的横坐标为8,求四边形
的横坐标为8,求四边形![]() 的面积
的面积
(3)定点![]() 在
在![]() 轴上,若将抛物线的图象向左平移2各单位,再向上平移3个单位得到一条新的抛物线,点
轴上,若将抛物线的图象向左平移2各单位,再向上平移3个单位得到一条新的抛物线,点![]() 在新的抛物线上运动,求定点
在新的抛物线上运动,求定点![]() 与动点
与动点![]() 之间距离的最小值
之间距离的最小值![]() (用含
(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
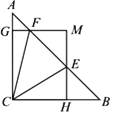
【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=![]() ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH=![]() ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH=![]() ,其中正确结论为( )
,其中正确结论为( )
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com