
【题目】在四边形ABCD中,∠B+∠D=180°,对角线AC平分∠BAD
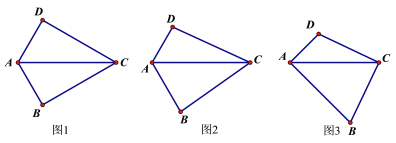
(1)如图1,若∠DAB=120°,且∠B=90°,易证AD+BA=AC
(2)如图2,若将(1)中的条件“∠B=90°”去掉,(1)中的结论是否成立?请说明理由.
(3)如图3,若∠DAB=90°,探究边AD、AB与对角线AC的数量关系并说明理由.
【答案】(1)见解析;(2)见解析;(3)AC=AD+AB,AD+AB=![]() AC.
AC.
【解析】
(1)结论:AC=AD+AB,只要证明AD=![]() AC,AB=
AC,AB=![]() AC即可解决问题;
AC即可解决问题;
(2)(1)中的结论成立.以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,只要证明△DAC≌△BEC即可解决问题;
(3)结论:AD+AB=![]() AC.过点C作CE⊥AC交AB的延长线于点E,只要证明△ACE是等腰直角三角形,△DAC≌△BEC即可解决问题;
AC.过点C作CE⊥AC交AB的延长线于点E,只要证明△ACE是等腰直角三角形,△DAC≌△BEC即可解决问题;
(1)AC=AD+AB.
理由如下:如图1中,
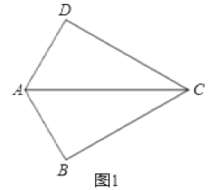
在四边形ABCD中,∠D+∠B=180°,∠B=90°,
∴∠D=90°,
∵∠DAB=120°,AC平分∠DAB,
∴∠DAC=∠BAC=60°,
∵∠B=90°,
∴AB=![]() AC,同理AD=
AC,同理AD=![]() AC.
AC.
∴AC=AD+AB.
(2)(1)中的结论成立,理由如下:以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,
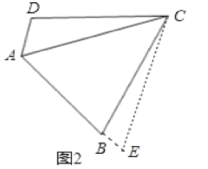
∵∠BAC=60°,
∴△AEC为等边三角形,
∴AC=AE=CE,
∵∠D+∠B=180°,∠DAB=120°,
∴∠DCB=60°,
∴∠DCA=∠BCE,
∵∠D+∠ABC=180°,∠ABC+∠EBC=180°,
∴∠D=∠CBE,∵CA=CB,
∴△DAC≌△BEC,
∴AD=BE,
∴AC=AD+AB.
(3)结论:AD+AB=![]() AC.理由如下:
AC.理由如下:
过点C作CE⊥AC交AB的延长线于点E,∵∠D+∠B=180°,∠DAB=90°,
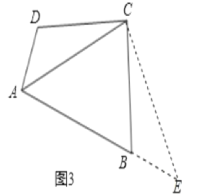
∴DCB=90°,
∵∠ACE=90°,
∴∠DCA=∠BCE,
又∵AC平分∠DAB,
∴∠CAB=45°,
∴∠E=45°.
∴AC=CE.
又∵∠D+∠B=180°,∠D=∠CBE,
∴△CDA≌△CBE,
∴AD=BE,
∴AD+AB=AE.
在Rt△ACE中,∠CAB=45°,
∴AE=![]() =
=![]() AC,
AC,
∴AD+AB=![]() AC.
AC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
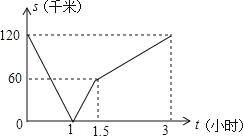
【题目】一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
①A、B两地相距60千米;
②出发1小时,货车与小汽车相遇;
③小汽车的速度是货车速度的2倍;
④出发1.5小时,小汽车比货车多行驶了60千米.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
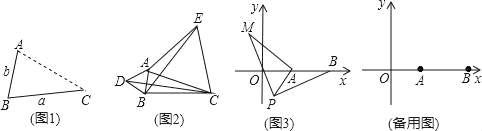
【题目】(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.填空:
当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示)
(2)应用:点A为线段BC外一动点,且BC=4,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;②直接写出线段BE长的最大值.
(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(6,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
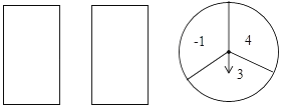
【题目】小红玩抽卡片和旋转盘游戏,有两张正面分别标有数字1,﹣2的不透明卡片,背面完全相同;转盘被平均分成3个相等的扇形,并分别标有数字﹣1,3,4(如图所示),小云把卡片背面朝上洗匀后从中随机抽出一张,记下卡片上的数字;然后转动转盘,转盘停止后,记下指针所在区域的数字(若指针在分格线上,则重转一次,直到指针指向某一区域为止).请用列表或树状图的方法(只选其中一种)求出两个数字之积为负数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保证人们上下楼的安全,楼梯踏步的宽度和高度都要加以限制.中小学楼梯宽度的范围是260mm~300mm含(300mm),高度的范围是120mm~150mm(含150mm).如图是某中学的楼梯扶手的截面示意图,测量结果如下:AB,CD分别垂直平分踏步EF,GH,各踏步互相平行,AB=CD,AC=900mm,∠ACD=65°,试问该中学楼梯踏步的宽度和高度是否符合规定.(结果精确到1mm,参考数据:sin65°≈0.906,cos65°≈0.423)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)如图,直线y=x+m和抛物线y=![]() +bx+c都经过点A(1,0),
+bx+c都经过点A(1,0),
B(3,2).

(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象,若直线y=2x+b与这个新图象有3个公共点,则b的值为( )
A. ﹣![]() 或﹣12B. ﹣
或﹣12B. ﹣![]() 或2C. ﹣12或2D. ﹣
或2C. ﹣12或2D. ﹣![]() 或﹣12
或﹣12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板按如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6cm,DC=7cm.把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点O、与D1E1相交于点F.
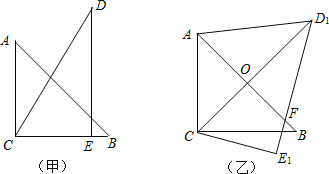
(1)求∠OFE1的度数;
(2)求线段AD1的长;
(3)若把△DCE绕着点C顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com