
ЁОЬтФПЁП(1)ЗЂЯжЃКШчЭМ1ЃЌЕуAЮЊЯпЖЮBCЭтвЛЖЏЕуЃЌЧвBCЃНaЃЌABЃНbЃЎЬюПеЃК
ЕБЕуAЮЛгкЁЁ ЁЁЪБЃЌЯпЖЮACЕФГЄШЁЕУзюДѓжЕЃЌЧвзюДѓжЕЮЊЁЁ ЁЁ(гУКЌaЃЌbЕФЪНзгБэЪО)
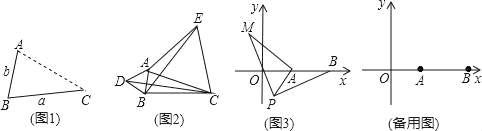
(2)гІгУЃКЕуAЮЊЯпЖЮBCЭтвЛЖЏЕуЃЌЧвBCЃН4ЃЌABЃН1ЃЌШчЭМ2ЫљЪОЃЌЗжБ№вдABЃЌACЮЊБпЃЌзїЕШБпШ§НЧаЮABDКЭЕШБпШ§НЧаЮACEЃЌСЌНгCDЃЌBEЃЎ
ЂйЧыевГіЭМжагыBEЯрЕШЕФЯпЖЮЃЌВЂЫЕУїРэгЩЃЛЂкжБНгаДГіЯпЖЮBEГЄЕФзюДѓжЕЃЎ
(3)ЭиеЙЃКШчЭМ3ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЕФзјБъЮЊ(2ЃЌ0)ЃЌЕуBЕФзјБъЮЊ(6ЃЌ0)ЃЌЕуPЮЊЯпЖЮABЭтвЛЖЏЕуЃЌЧвPAЃН2ЃЌPMЃНPBЃЌЁЯBPMЃН90ЁуЃЌЧыжБНгаДГіЯпЖЮAMГЄЕФзюДѓжЕМАДЫЪБЕуPЕФзјБъЃЎ
ЁОД№АИЁП(1)CBЕФбгГЄЯпЩЯЃЌ a+bЃЛ(2)ЂйCDЃНBEЃЌРэгЩМћНтЮіЃЛЂкBEГЄЕФзюДѓжЕЮЊ5ЃЛ(3)ТњзуЬѕМўЕФЕуPзјБъ(2Љ![]() ЃЌ
ЃЌ![]() )Лђ(2Љ
)Лђ(2Љ![]() ЃЌЉ
ЃЌЉ![]() )ЃЌAMЕФзюДѓжЕЮЊ2
)ЃЌAMЕФзюДѓжЕЮЊ2![]() +4ЃЎ
+4ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕуAЮЛгкCBЕФбгГЄЯпЩЯЪБЃЌЯпЖЮACЕФГЄШЁЕУзюДѓжЕЃЌМДПЩЕУЕННсТлЃЛЃЈ2ЃЉЂйИљОнвбжЊЬѕМўвзжЄЁїCADЁеЁїEABЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪМДПЩЕУCDЃНBEЃЛЂкгЩгкЯпЖЮBEГЄЕФзюДѓжЕЃНЯпЖЮCDЕФзюДѓжЕЃЌИљОнЃЈ1ЃЉжаЕФНсТлМДПЩЕУЕННсЙћЃЛЃЈ3ЃЉСЌНгBMЃЌНЋЁїAPMШЦзХЕуPЫГЪБеыа§зЊ90ЁуЕУЕНЁїPBNЃЌСЌНгANЃЌЕУЕНЁїAPNЪЧЕШбќжБНЧШ§НЧаЮЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНPNЃНPAЃН2ЃЌBNЃНAMЃЌИљОнЕБNдкЯпЖЮBAЕФбгГЄЯпЪБЃЌЯпЖЮBNШЁЕУзюДѓжЕЃЌМДПЩЕУЕНзюДѓжЕЮЊ2![]() +4ЃЛШчЭМ2ЃЌЙ§PзїPEЁЭxжсгкEЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪМДПЩЧѓЕУЕуPЕФзјБъЃЎШчЭМ3жаЃЌИљОнЖдГЦадПЩжЊЕБЕуPдкЕкЫФЯѓЯоЪБвВТњзуЬѕМўЃЌгЩДЫЧѓЕУЗћКЯЬѕМўЕФЕуPСэвЛИіЕФзјБъЃЎ
+4ЃЛШчЭМ2ЃЌЙ§PзїPEЁЭxжсгкEЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪМДПЩЧѓЕУЕуPЕФзјБъЃЎШчЭМ3жаЃЌИљОнЖдГЦадПЩжЊЕБЕуPдкЕкЫФЯѓЯоЪБвВТњзуЬѕМўЃЌгЩДЫЧѓЕУЗћКЯЬѕМўЕФЕуPСэвЛИіЕФзјБъЃЎ
(1)ЁпЕуAЮЊЯпЖЮBCЭтвЛЖЏЕуЃЌЧвBCЃНaЃЌABЃНbЃЌ
ЁрЕБЕуAЮЛгкCBЕФбгГЄЯпЩЯЪБЃЌЯпЖЮACЕФГЄШЁЕУзюДѓжЕЃЌЧвзюДѓжЕЮЊBC+ABЃНa+bЃЌ
ЙЪД№АИЮЊЃКCBЕФбгГЄЯпЩЯЃЌa+bЃЛ
(2)ЂйCDЃНBEЃЌ
РэгЩЃКЁпЁїABDгыЁїACEЪЧЕШБпШ§НЧаЮЃЌ
ЁрADЃНABЃЌACЃНAEЃЌЁЯBADЃНЁЯCAEЃН60ЁуЃЌ
ЁрЁЯBAD+ЁЯBACЃНЁЯCAE+ЁЯBACЃЌ
МДЁЯCADЃНЁЯEABЃЌ
дкЁїCADгыЁїEABжаЃЌ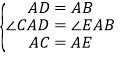 ЃЌ
ЃЌ
ЁрЁїCADЁеЁїEAB(SAS)ЃЌ
ЁрCDЃНBEЃЛ
ЂкЁпЯпЖЮBEГЄЕФзюДѓжЕЃНЯпЖЮCDЕФзюДѓжЕЃЌ
гЩ(1)жЊЃЌЕБЯпЖЮCDЕФГЄШЁЕУзюДѓжЕЪБЃЌЕуDдкCBЕФбгГЄЯпЩЯЃЌ
ЁрзюДѓжЕЮЊBD+BCЃНAB+BCЃН5ЃЛ
(3)ШчЭМ1ЃЌ
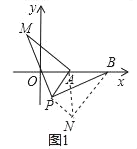
ЁпНЋЁїAPMШЦзХЕуPЫГЪБеыа§зЊ90ЁуЕУЕНЁїPBNЃЌСЌНгANЃЌ
дђЁїAPNЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрPNЃНPAЃН2ЃЌBNЃНAMЃЌ
ЁпAЕФзјБъЮЊ(2ЃЌ0)ЃЌЕуBЕФзјБъЮЊ(6ЃЌ0)ЃЌ
ЁрOAЃН2ЃЌOBЃН6ЃЌ
ЁрABЃН4ЃЌ
ЁрЯпЖЮAMГЄЕФзюДѓжЕЃНЯпЖЮBNГЄЕФзюДѓжЕЃЌ
ЁрЕБNдкЯпЖЮBAЕФбгГЄЯпЪБЃЌЯпЖЮBNШЁЕУзюДѓжЕЃЌ
зюДѓжЕЃНAB+ANЃЌ
ЁпANЃН![]() APЃН2
APЃН2![]() ЃЌ
ЃЌ
ЁрзюДѓжЕЮЊ2![]() +4ЃЛ
+4ЃЛ
ШчЭМ2ЃЌ
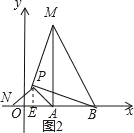
Й§PзїPEЁЭxжсгкEЃЌ
ЁпЁїAPNЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрPEЃНAEЃН![]() ЃЌ
ЃЌ
ЁрOEЃНBOЉABЉAEЃН6Љ4Љ![]() ЃН2Љ
ЃН2Љ![]() ЃЌ
ЃЌ
ЁрP(2Љ![]() ЃЌ
ЃЌ![]() )ЃЎ
)ЃЎ
ШчЭМ3жаЃЌ
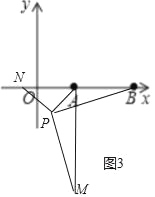
ИљОнЖдГЦадПЩжЊЕБЕуPдкЕкЫФЯѓЯоЪБЃЌP(2Љ![]() ЃЌЉ
ЃЌЉ![]() )ЪБЃЌвВТњзуЬѕМўЃЎ
)ЪБЃЌвВТњзуЬѕМўЃЎ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуPзјБъ(2Љ![]() ЃЌ
ЃЌ![]() )Лђ(2Љ
)Лђ(2Љ![]() ЃЌЉ
ЃЌЉ![]() )ЃЌAMЕФзюДѓжЕЮЊ2
)ЃЌAMЕФзюДѓжЕЮЊ2![]() +4ЃЎ
+4ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxoyжаЃЌжБЯп![]() гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуB.ЖЏЕуPЁЂQЗжБ№ДгOЁЂBЭЌЪБГіЗЂЃЌЦфжаЕуPвдУПУы4ИіЕЅЮЛЕФЫйЖШбиOBЯђжеЕуBдЫЖЏ,ЕуQвдУПУы5ИіЕЅЮЛЕФЫйЖШбиBAЯђжеЕуAдЫЖЏ.ЩшдЫЖЏЪБМфЮЊtУы.
гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуB.ЖЏЕуPЁЂQЗжБ№ДгOЁЂBЭЌЪБГіЗЂЃЌЦфжаЕуPвдУПУы4ИіЕЅЮЛЕФЫйЖШбиOBЯђжеЕуBдЫЖЏ,ЕуQвдУПУы5ИіЕЅЮЛЕФЫйЖШбиBAЯђжеЕуAдЫЖЏ.ЩшдЫЖЏЪБМфЮЊtУы.
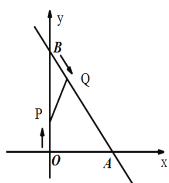
(1)СЌНсPQЃЌШєЁїAOBКЭвдBЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮЯрЫЦЃЌЧѓtЕФжЕЃЛ
(2)СЌНсAPЁЂOQЃЌШєAPЁЭOQЃЌЧѓtЕФжЕЃЛ
(3)ЪджЄУїЃКPQЕФжаЕудкЁїAOBЕФвЛЬѕжаЮЛЯпЩЯ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃК
вбжЊЪЕЪ§mЃЌnТњзу(2m2ЃЋn2ЃЋ1)(2m2ЃЋn2Ѓ1)ЃН80ЃЌЪдЧѓ2m2ЃЋn2ЕФжЕ.
НтЃКЩш2m2ЃЋn2ЃНtЃЌдђдЗНГЬБфЮЊ(tЃЋ1)(tЃ1)ЃН80ЃЌећРэЕУt2Ѓ1ЃН80ЃЌt2ЃН81ЃЌ
ЫљвдtЃНЭС9ЃЌвђЮЊ2m2ЃЋn2ЃО0ЃЌЫљвд2m2ЃЋn2ЃН9.
ЩЯУцетжжЗНЗЈГЦЮЊЁАЛЛдЊЗЈЁБЃЌАбЦфжаФГаЉВПЗжПДГЩвЛИіећанЃЌВЂгУаТзжФИДњЬц(МДЛЛдЊ)ЃЌдђФмЪЙИДдгЕФЮЪЬтМђЕЅЛЏ.
ИљОнвдЩЯдФЖСВФСЯФкШнЃЌНтОіЯТСаЮЪЬтЃЌВЂаДГіНтД№Й§ГЬ.
ЃЈ1ЃЉвбжЊЪЕЪ§xЁЂyЃЌТњзу(2x2ЃЋ2y2ЃЋ3)(2x2ЃЋ2y2Ѓ3)ЃН27ЃЌЧѓx2ЃЋy2ЕФжЕ.
ЃЈ2ЃЉвбжЊRtЁїACBЕФШ§БпЮЊaЁЂbЁЂcЃЈcЮЊаББпЃЉЃЌЦфжаaЁЂbТњзу(a2ЃЋb2)(a2ЃЋb2Ѓ4)ЃН5ЃЌЧѓRtЁїACBЭтНгдВЕФАыОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкЦНУцжБНЧзјБъЯЕжа,вдЕуM(0,![]() )ЮЊдВаФ,вд
)ЮЊдВаФ,вд![]() ГЄЮЊАыОЖзїMНЛxжсгкA.BСНЕуЃЌНЛyжсгкC.DСНЕуЃЌСЌНгAMВЂбгГЄНЛMгкPЕуЃЌСЌНгPCНЛxжсгкE.
ГЄЮЊАыОЖзїMНЛxжсгкA.BСНЕуЃЌНЛyжсгкC.DСНЕуЃЌСЌНгAMВЂбгГЄНЛMгкPЕуЃЌСЌНгPCНЛxжсгкE.
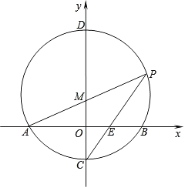
(1)ЧѓЕуC.PЕФзјБъЃЛ
(2)ЧѓжЄЃКBE=2OE.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
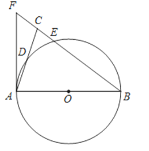
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌBA=BCЃЌвдABЮЊжБОЖЕФЁбOЗжБ№НЛACЃЌBCгкЕуDЃЌEЃЌBCЕФбгГЄЯпгыЁбOЕФЧаЯпAFНЛгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯABC=2ЁЯCAFЃЛ
ЃЈ2ЃЉШєAC=2![]() ЃЌCEЃКEB=1ЃК4ЃЌЧѓCEЃЌAFЕФГЄЃЎ
ЃЌCEЃКEB=1ЃК4ЃЌЧѓCEЃЌAFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
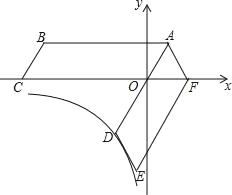
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCOЪЧЦНааЫФБпаЮЃЌOA=2ЃЌAB=6ЃЌЕуCдкxжсЕФИКАыжсЩЯЃЌНЋЦНааЫФБпаЮ ABCOШЦЕуAФцЪБеыа§зЊЕУЕНЦНааЫФБпаЮADEFЃЌADОЙ§ЕуOЃЌЕуFЧЁКУТфдкxжсЕФе§АыжсЩЯЃЎШєЕуDдкЗДБШР§КЏЪ§y=![]() ЃЈxЃМ0ЃЉЕФЭМЯѓЩЯЃЌдђkЕФжЕЮЊЃЈЁЁЁЁЃЉ
ЃЈxЃМ0ЃЉЕФЭМЯѓЩЯЃЌдђkЕФжЕЮЊЃЈЁЁЁЁЃЉ
A.4![]() B.12C.8
B.12C.8![]() D.6
D.6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
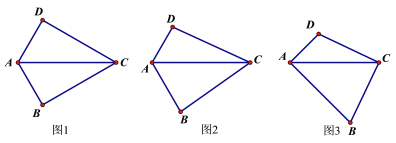
ЁОЬтФПЁПдкЫФБпаЮABCDжа,ЁЯB+ЁЯD=180Ёу,ЖдНЧЯпACЦНЗжЁЯBAD
(1)ШчЭМ1,ШєЁЯDAB=120Ёу,ЧвЁЯB=90Ёу,взжЄAD+BAЃНAC
(2)ШчЭМ2,ШєНЋ(1)жаЕФЬѕМўЁАЁЯB=90ЁуЁБШЅЕє,(1)жаЕФНсТлЪЧЗёГЩСЂ?ЧыЫЕУїРэгЩ.
(3)ШчЭМ3,ШєЁЯDAB=90Ёу,ЬНОПБпADЁЂABгыЖдНЧЯпACЕФЪ§СПЙиЯЕВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
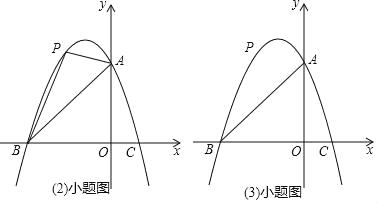
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌХзЮяЯпyЃНax2+bx+3гызјБъжсЗжБ№НЛгкЕуAЃЌBЃЈЉ3ЃЌ0ЃЉЃЌCЃЈ1ЃЌ0ЃЉЃЌЕуPЪЧЯпЖЮABЩЯЗНХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉЕБЕуPдЫЖЏЕНЪВУДЮЛжУЪБЃЌЁїPABЕФУцЛ§зюДѓЃП
ЃЈ3ЃЉЙ§ЕуPзїxжсЕФДЙЯпЃЌНЛЯпЖЮABгкЕуDЃЌдйЙ§ЕуPзїPEЁЮxжсНЛХзЮяЯпгкЕуEЃЌСЌНгDEЃЌЧыЮЪЪЧЗёДцдкЕуPЪЙЁїPDEЮЊЕШбќжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓЕуPЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
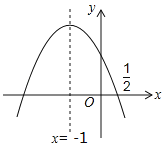
ЁОЬтФПЁПЃЈ4ЗжЃЉШчЭМЃЌХзЮяЯп![]() ЕФЖдГЦжсЪЧ
ЕФЖдГЦжсЪЧ![]() ЃЎЧвЙ§ЕуЃЈ
ЃЎЧвЙ§ЕуЃЈ![]() ЃЌ0ЃЉЃЌгаЯТСаНсТлЃКЂйabcЃО0ЃЛЂкaЉ2b+4c=0ЃЛЂл25aЉ10b+4c=0ЃЛЂм3b+2cЃО0ЃЛЂнaЉbЁнmЃЈamЉbЃЉЃЛЦфжаЫљгае§ШЗЕФНсТлЪЧ ЃЎЃЈЬюаДе§ШЗНсТлЕФађКХЃЉ
ЃЌ0ЃЉЃЌгаЯТСаНсТлЃКЂйabcЃО0ЃЛЂкaЉ2b+4c=0ЃЛЂл25aЉ10b+4c=0ЃЛЂм3b+2cЃО0ЃЛЂнaЉbЁнmЃЈamЉbЃЉЃЛЦфжаЫљгае§ШЗЕФНсТлЪЧ ЃЎЃЈЬюаДе§ШЗНсТлЕФађКХЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com