练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图是二次函数y＝ax2+bx+c（a≠0）的图象的一部分，给出下列命题：①a+b+c＝0；②b＞2a；③ax2+bx+c＝0的两根分别为﹣3和1；④a﹣2b+c＞0，其中正确的命题是（ ）

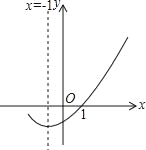
    A. ①②③B. ①③C. ①④D. ①③④

    【答案】B

    【解析】

    根据抛物线经过（1，0），确定a+b+c的符号；根据对称轴方程确定b与2a的关系；根据抛物线与x轴的一个交点和对称轴确定另一个交点，得到ax2+bx+c＝0的两根；根据a＞0，b＞0，c＜0，b＝2a，确定a﹣2b+c的符号．

    解：∵y＝ax2+bx+c经过（1，0），

    ∴a+b+c＝0，①正确；

    ∵

    ∴b＝2a，②错误；

    ∵y＝ax2+bx+c经过（1，0），对称轴为x＝﹣1，

    ∴y＝ax2+bx+c与x轴的另一个交点为（﹣3，0），

    ∴ax2+bx+c＝0的两根分别为﹣3和1，③正确；

    ∵a＞0，b＞0，c＜0，b＝2a，

    ∴a﹣2b+c＝﹣a﹣b+c＜0，④错误，

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（2011山东济南，27，9分）如图，矩形OABC中，点O为原点，点A的坐标为（0，8），点C的坐标为（6，0）．抛物线经过A、C两点，与AB边交于点D．

    （1）求抛物线的函数表达式；

    （2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ=CP，连接PQ，设CP=m，△CPQ的面积为S．

    ①求S关于m的函数表达式，并求出m为何值时，S取得最大值；

    ②当S最大时，在抛物线的对称轴l上若存在点F，使△FDQ为直角三角形，请直接写出所有符合条件的F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】函数y＝的图象与直线y＝x+1没有交点，那么k的取值范围是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是2019年1月份的日历．任意选择图中的菱形框部分，将每个菱形框部分中去掉中间位置的数之后，相对的两对数分别相乘，再相减，例如：9×11-3×17=48，13×15-7×21=48．不难发现，结果都是48

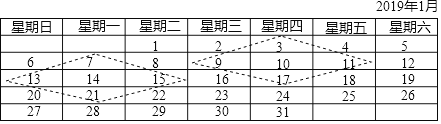
    （1）请证明发现的规律；

    （2）小明说：他用一个如图所示菱形框，框出5个数字，其中最小数与最大数的积是120，请判断他的说法是否正确．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，点D是弧AE上一点，且∠BDE=∠CBE，BD与AE交于点F.

    （1）求证：BC是⊙O的切线；

    （2）若BD平分∠ABE，求证：DE2=DF·DB；

    （3）在（2）的条件下，延长ED，BA交于点P，若PA=AO，DE=2，求PD的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将二次函数y＝x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新图象，若直线y＝2x+b与这个新图象有3个公共点，则b的值为（　　）

    A. ﹣或﹣12B. ﹣或2C. ﹣12或2D. ﹣或﹣12

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC中，∠C＝90°，AC＝4π，BC＝3π，半径是2的⊙O从与AC相切于点D的位置出发，在△ABC外部按顺时针方向沿三角形滚动，又回到与AC相切于点D的位置，则⊙O自转了（　　）

    A.2周B.3周C.4周D.5周

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1所示，点E在弦AB所对的优弧上，且为半圆，C是上的动点，连接CA、CB，已知AB＝4cm，设B、C间的距离为xcm，点C到弦AB所在直线的距离为y1cm，A、C两点间的距离为y2cm．

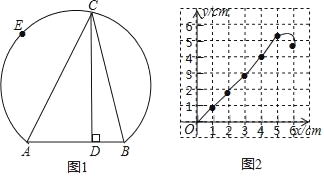
    小明根据学习函数的经验，分别对函数y1、y2岁自变量x的变化而变化的规律进行了探究．下面是小明的探究过程，请补充完整．

    （1）按照下表中自变量x的值进行取点、画图、测量，分别得到了y1、y2与x的几组对应值：

    x/cm

    0

    1

    2

    3

    4

    5

    6

    y1/cm

    0

    0.78

    1.76

    2.85

    3.98

    4.95

    4.47

    y2/cm

    4

    4.69

    5.26

    5.96

    5.94

    4.47

    （2）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x，y1），（x，y2），并画出函数y1、y2的图象；

    （3）结合函数图象，解决问题：

    ①连接BE，则BE的长约为　 　cm．

    ②当以A、B、C为顶点组成的三角形是直角三角形时，BC的长度约为　 　cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2-4n+4经过点P（2,4），与x轴交于A、B两点，过点P作直线l∥x轴，点C为第二象限内直线l上方，抛物线上一个动点，其横坐标为m。

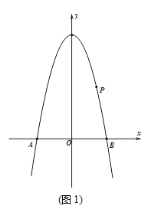
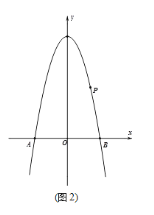
    （1）如图（1），若AB=6, 求抛物线解析式

    （2）如图（2），在（1）的条件下，设点C的横坐标为t,ACP的面积S，求S与t之间的函数关系式.

    （3）如图（3），连接OP，过点C作EC∥OP交抛物线于点E，直线PE、CP分别交x轴于点G、H，当PG=PH时，求a的值。

    查看答案和解析>>

    同步练习册答案