练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．一次函数y=-$\frac{1}{2}$kx-2k的图象可能是（　　）
    A．B．C．D．

    分析 根据图象与x轴的交点直接解答即可．

    解答 解：令y=0，则函数y=-$\frac{1}{2}$kx-2k的图象与y轴交于点（-4，0），
    故图象与x轴的交点在x轴的负半轴上．
    故选C．

    点评 本题考查一次函数的图象，熟知一次函数的图象与x轴交点的特点是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    3．如图，直线a与直线b交于点A，与直线c交于点B，∠1=120°，∠2=40°，若使直线b与直线c平行，则可将直线b绕点A逆时针旋转20°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图所示，分别以Rt△ABC的直角边AC，斜边AB为边向△ABC外构造等边△ACD和等边△ABE，F为AB的中点，连接DF，EF，∠ACB=90°，∠ABC=30°．有下列四个结论：①AC⊥DF；②四边形BCDF为平行四边形；③DA+DF=BE；④$\frac{{S}_{△ACD}}{{S}_{四边形BCDE}}$=$\frac{1}{6}$．其中正确的结论是①②（填写正确结论的序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．一次函数y1=ax+b与一次函数y2=-bx-a在同一平面直角坐标系中的图象大致是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，点M为正方形ABCD的边AB（或BA）延长线上任意一点，MN⊥DM且与∠ABC外角的平分线交于点N，此时MD与MN有何数量关系？并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．一块三角形纸板ABC，∠ACB=90°，AC=3，AB=5，把它置于平面直角坐标系中，AC∥y轴，BC∥x轴，顶点A，B恰好都在反比例函数y=$\frac{k}{x}$的图象上，AC，BC的延长线分别交x轴、y轴于D，E两点，设点C的坐标为（m，n）．
    （1）求A，B两点的坐标（含m，n，不含k）；
    （2）当m=n+0.5时，求该反比例函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，已知直线y=kx+b与双曲线y=$\frac{m}{x}$（x＜0）交于A（x1，y1），B（x2，y2），且x1≠x2，直线AB交x轴于点C（x0，0）．
    （1）若A（-1，4），B（-2，y2），求直线AB的解析式及C点的坐标；
    （2）若C（-4，0），B（-3，1），求A点的坐标；
    （3）设点M（$\frac{{x}_{1}+{x}_{2}}{2}$，$\frac{{y}_{1}+{y}_{2}}{2}$）为线段AB的中点，记$\frac{{x}_{1}+{x}_{2}}{2}$=t，直接写出t与x0之间的关系为x0=2t．（不要求证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，点A，B，C，D为⊙O上的四个点，$\widehat{BC}$=$\widehat{CD}$，AC交BD于点E，CE=4，CD=6．
    （1）求证：△CDE∽△CAD；
    （2）求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

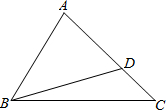    8．如图：△ABC中，∠C=45°，点D在AC上，且∠ADB=60°，AB为△BCD外接圆的切线．
    （1）用尺规作出△BCD的外接圆（保留作图痕迹，可不写作法）；
    （2）求∠A的度数；
    （3）求$\frac{AD}{DC}$的值．

    查看答案和解析>>

    同步练习册答案