
【题目】如图,已知矩形![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以每秒1个单位的速度运动,连接
方向以每秒1个单位的速度运动,连接![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() .
.
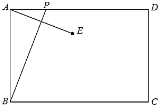
(1)若![]() ,
,![]() 仅在边
仅在边![]() 运动,求当
运动,求当![]() ,
,![]() ,
,![]() 三点在同一直线上时对应的
三点在同一直线上时对应的![]() 的值.
的值.
(2)在动点![]() 在射线
在射线![]() 上运动的过程中,求使点
上运动的过程中,求使点![]() 到直线
到直线![]() 的距离等于3时对应的
的距离等于3时对应的![]() 的值.
的值.
【答案】(1)![]() 时,
时,![]() 、
、![]() 、
、![]() 共线;(2)
共线;(2)![]() 或
或![]()
【解析】
(1)设AP=t,则PD=6﹣t,由点A、E关于直线BP对称,得出∠APB=∠BPE,由平行线的性质得出∠APB=∠PBC,得出∠BPC=∠PBC,在Rt△CDP中,由勾股定理得出方程,解方程即可得出结果;
(2)①当点E在BC的上方,点E到BC的距离为3,作EM⊥BC于M,延长ME交AD于N,连接PE、BE,则EM=3,EN=1,BE=AB=4,四边形ABMN是矩形,AN=BM=![]() ,证出△BME∽△ENP,得出
,证出△BME∽△ENP,得出![]() ,求出NP=
,求出NP=![]() ,即可得出结果;
,即可得出结果;
②当点E在BC的下方,点E到BC的距离为3,作EH⊥AB的延长线于H,则BH=3,BE=AB=4,AH=AB+BH=7,HE=![]() ,证得△AHE∽△PAB,得出
,证得△AHE∽△PAB,得出![]() ,即可得出结果.
,即可得出结果.
解:(1)设AP=t,则PD=6﹣t,如图1所示:
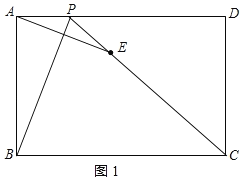
∵点A、E关于直线BP对称,
∴∠APB=∠BPE,
∵AD∥BC,
∴∠APB=∠PBC,
∵P、E、C共线,
∴∠BPC=∠PBC,
∴CP=BC=AD=6,
在Rt△CDP中,CD2+DP2=PC2,
即:42+(6﹣t)2=62,
解得:t=6﹣2![]() 或6+2
或6+2![]() (不合题意舍去),
(不合题意舍去),
∴t=(6﹣2![]() )s时,P、E、C共线;
)s时,P、E、C共线;
(2)①当点E在BC的上方,点E到BC的距离为3,作EM⊥BC于M,延长ME交AD于N,连接PE、BE,如图2所示:
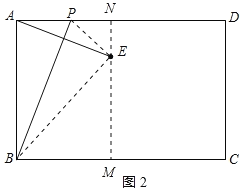
则EM=3,EN=1,BE=AB=4,四边形ABMN是矩形,
在Rt△EBM中,AN=BM=![]() ,
,
∵点A、E关于直线BP对称,
∴∠PEB=∠PAB=90°,
∵∠ENP=∠EMB=∠PEB=90°,
∴∠PEN=∠EBM,
∴△BME∽△ENP,
∴![]() ,即
,即![]() ,
,
∴NP=![]() ,
,
∴t=AP=AN﹣NP=![]() ;
;
②当点E在BC的下方,点E到BC的距离为3,作EH⊥AB的延长线于H,如图3所示:

则BH=3,BE=AB=4,AH=AB+BH=7,
在Rt△BHE中,HE=![]() ,
,
∵∠PAB=∠BHE=90°,AE⊥BP,
∴∠APB+∠EAP=∠HAE+∠EAP=90°,
∴∠HAE=∠APB,
∴△AHE∽△PAB,
∴![]() ,即
,即![]() ,
,
解得:t=AP=4![]() ,
,
综上所述,t=![]() 或4
或4![]() .
.


科目:初中数学 来源: 题型:
【题目】2015年12月16﹣18日,第二届互联网大会在浙江乌镇胜利举行,这说明我国互联网发展走到了世界的前列,尤其是电子商务.据市场调查,天猫超市在销售一种进价为每件40元的护眼台灯中发现:每月销售量y(件)与销售单价x(元)之间的函数关系如图所示.
(1)当销售单价定为50元时,求每月的销售件数;
(2)设每月获得利润为w(元),求每月获得利润w(元)关于销售单价x(元)的函数解析式;
(3)由于市场竞争激烈,这种护眼灯的销售单价不得高于75元,如果要每月获得的利润不低于8000元,那么每月的成本最少需要多少元?(成本=进价×销售量)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县在一次九年级数学模拟测试中,有一道满分为8分的解答题,按评分标准,所有考生的得分只有四种情况:0分、3分、5分、8分.老师为了了解学生的得分情况与题目的难易程度,从全县9000名考生的试卷中随机抽取若干份,通过分析与整理,绘制了如下两幅不完整的统计图.
九年级数学质量检测一道解答题学生得分情况统计图
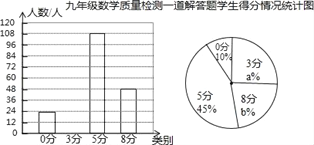
请根据以上信息解答下列问题:
(1)该题学生得分情况的众数是 .
(2)求所抽取的试卷份数,并补全条形统计图.
(3)已知难度系数的计算公式为![]() ,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0≤L<0.5时,此题为难题;当0.5≤L≤0.8时,此题为中等难度试题;当0.8<L≤1时,此题为容易题.通过计算,说明此题对于该县的九年级学生来说属于哪一类?
,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0≤L<0.5时,此题为难题;当0.5≤L≤0.8时,此题为中等难度试题;当0.8<L≤1时,此题为容易题.通过计算,说明此题对于该县的九年级学生来说属于哪一类?
查看答案和解析>>
科目:初中数学 来源: 题型:
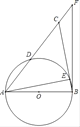
【题目】如图,在等腰△ABC中,AB=BC,以AB为直径的半圆分别交AC、BC于点D、E两点,BF与⊙O相切于点B,交AC的延长线于点F.
(1)求证:D是AC的中点;
(2)若AB=12,sin∠CAE=![]() ,求CF的值.
,求CF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】佳佳调査了七年级400名学生到校的方式,根据调查结果绘制出统计图的一部分如图:
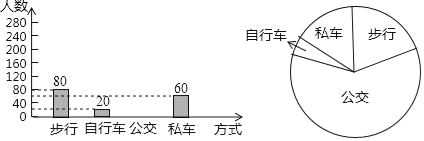
(1)补全条形统计图;
(2)求扇形统计图中表示“步行”的扇形圆心角的度数;
(3)估计在3000名学生中乘公交的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“小组合作制”正在七年级如火如茶地开展,旨在培养七年级学生的合作学习的精神和能力,学会在合作中自主探索.数学课上,吴老师在讲授“角平分线”时,设计了如下四种教学方法:①教师讲授,学生练习;②学生合作交流,探索规律;③教师引导学生总结规律,学生练习;④教师引导学生总结规律,学生合作交流,吴老师将上述教学方法作为调研内容发到七年级所有同学手中要求每位同学选出自己最喜欢的一种,然后吴老师从所有调查问卷中随机抽取了若干份调查问卷作为样本,统计如下:
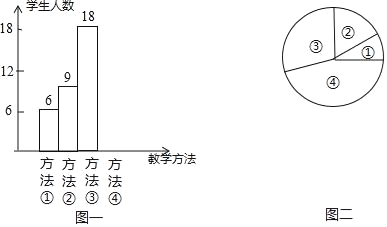
序号①②③④代表上述四种教学方法,图二中,表示①部分的扇形的中心角度数为36°,请回答问题:
(1)在后来的抽样调查中,吴老师共抽取 位学生进行调查;并将条形统计图补充完整;
(2)图二中,表示③部分的扇形的中心角为多少度?
(3)若七年级学生中选择④种教学方法的有540人,请估计七年级总人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
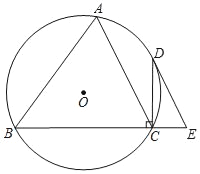
【题目】如图,△ABC内接于⊙O,过点C作BC的垂线交⊙O于D,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求⊙O直径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+c与x轴交于点B(4,0),与y轴交于点C,抛物线y=
x+c与x轴交于点B(4,0),与y轴交于点C,抛物线y=![]() x2+bx+c经过点B,C,与x轴的另一个交点为点A.
x2+bx+c经过点B,C,与x轴的另一个交点为点A.
(1)求抛物线的解析式;
(2)点P是直线BC下方的抛物线上一动点,求四边形ACPB的面积最大时点P的坐标;
(3)若点M是抛物线上一点,请直接写出使∠MBC=![]() ∠ABC的点M的坐标.
∠ABC的点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com