
 如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进120米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进120米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )| A. | $60\sqrt{3}$ | B. | 61 | C. | $60\sqrt{3}+1$ | D. | 121 |
 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上,
△ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=mx2+2(m+2)x+m+9.
已知二次函数y=mx2+2(m+2)x+m+9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
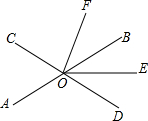 如图,直线AB,CD相交于点O,OE平分∠BOD.
如图,直线AB,CD相交于点O,OE平分∠BOD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直径AB、CD所夹锐角为60°,点P为$\widehat{BC}$上的一个动点(不与点B、C重合),PM、PN分别垂直于CD、AB,垂足分别为点M、N.若⊙O的半径为2cm,则在点P移动过程中,MN的长是否有变化否(填“是”或“否”),若有变化,写出MN的长度范围;若无变化,写出MN的长度:$\sqrt{3}$cm.
如图,直径AB、CD所夹锐角为60°,点P为$\widehat{BC}$上的一个动点(不与点B、C重合),PM、PN分别垂直于CD、AB,垂足分别为点M、N.若⊙O的半径为2cm,则在点P移动过程中,MN的长是否有变化否(填“是”或“否”),若有变化,写出MN的长度范围;若无变化,写出MN的长度:$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{1}{8}$ | C. | -$\frac{1}{8}$ | D. | -$\frac{3}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com