
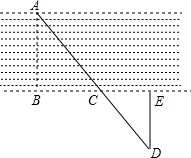
 为了测量一条小河的宽度,小明所在小组同学决定选取河对岸岸边某处为A点,在同侧岸边选取B,C,E三点,使B,C,E在同一直线上,且AB与BE垂直.再过点E作DE⊥BE交AC的延长线于点D,并测得BC=15m,CE=3m,DE=5.4m,则河的宽度AB约为( )
为了测量一条小河的宽度,小明所在小组同学决定选取河对岸岸边某处为A点,在同侧岸边选取B,C,E三点,使B,C,E在同一直线上,且AB与BE垂直.再过点E作DE⊥BE交AC的延长线于点D,并测得BC=15m,CE=3m,DE=5.4m,则河的宽度AB约为( )| A. | 21m | B. | 24m | C. | 27m | D. | 8.6m |
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | 0°<∠A<30° | B. | 30°<∠A<45° | C. | 45°<∠A<60° | D. | 60°<∠A<90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 数量x(千克) | 1 | 2 | 3 | 4 | … |
| 售价y(元) | 8+0.4 | 16+0.8 | 24+1.2 | 32+1.6 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
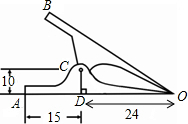 如图是一个常见铁夹的剖面图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA,垂足为D,DA=15mm,DO=24mm,DC=10mm,且铁夹的剖面图是轴对称图形,求A,B两点间的距离.
如图是一个常见铁夹的剖面图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA,垂足为D,DA=15mm,DO=24mm,DC=10mm,且铁夹的剖面图是轴对称图形,求A,B两点间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com