
【题目】如图,矩形ABCD中,AB=8,BC=4,O为对角线AC的中点,点P,Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B,C,连接PO,QO并延长分别与CD,DA交于点M,N,在整个运动过程中,图中阴影部分面积的大小变化情况是( )
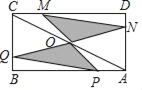
A. 一直增大 B. 一直减小 C. 先减小后增大 D. 先增大后减小
【答案】C
【解析】分析:过O作OE⊥AB于E,OF⊥BC于F,设BQ=x,由点P的速度是点Q的速度2倍,设AP=2x,BP=8﹣2x,CQ=4﹣x,用含x的代数式表示阴影部分的面积,根据函数的性质判断.
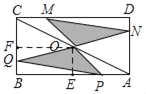
详解:如图所示,过O作OE⊥AB于E,OF⊥BC于F,
∵矩形ABCD中,AB=8,BC=4,O为对角线AC的中点,
∴OE=![]() BC=2,OF=
BC=2,OF=![]() AB=4,
AB=4,
设BQ=x,则由点P的速度是点Q的速度2倍,可得AP=2x,BP=8﹣2x,CQ=4﹣x,
∵△POQ的面积=Rt△ABC的面积﹣△AOP的面积﹣△COQ的面积﹣△BPQ的面积
=![]() ×4×8﹣
×4×8﹣![]() ×2x×2﹣
×2x×2﹣![]() ×(4﹣x)×4﹣
×(4﹣x)×4﹣![]() x(8﹣2x)
x(8﹣2x)
=x2﹣4x+8,
∴阴影部分面积y=2x2﹣8x+16(0≤x≤4),
∴当x=2时,阴影部分面积y有最小值,
根据二次函数的性质,可得阴影部分面积先减小后增大,
故选C.


科目:初中数学 来源: 题型:
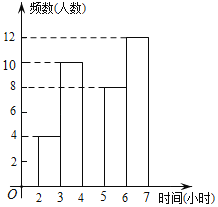
【题目】滨海新区某中学为了了解学生每周在校体育锻炼的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了不完整的统计图表,请根据图表信息解答下列问题
时间(小时) | 频数(人数) | 百分比 |
2≤t<3 | 4 | 10% |
3≤t<4 | 10 | 25% |
4≤t<5 | a | 15% |
5≤t<6 | 8 | b% |
6≤t<7 | 12 | 30% |
合计 | 40 | 100% |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若绘制扇形统计图,时间段6≤x<7所对应扇形的圆心角的度数是多少?
(4)若该校共有1200名学生,估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
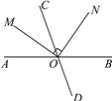
【题目】如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.
(1)若∠BOD=70°,求∠AOM和∠CON的度数;
(2)若∠BON=50°,求∠AOM和∠CON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,3),反比例函数y=![]() 的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
(1)求反比例函数的解析式;
(2)通过计算说明一次函数y=mx+3﹣4m的图象一定过点C;
(3)对于一次函数y=mx+3﹣4m(m≠0),当y随x的增大而增大时,确定点P的横坐标的取值范围,(不必写过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司的某种产品由一家商店代销,双方协议不论这种产品的销售情况如何,该公司每月都要付给商店a元代销费,同时商店每销售一件产品有b元提成.该商店一月份销售了m件,二月份销售了n件.
(1)用代数式表示这两个月公司应付给商店的代销总金额;
(2)假设代销费为每月200元,每件产品的提成为2元,该商店一月份销售了200件,二月份销售了260件,求该商店这两个月销售此种产品的收益.
查看答案和解析>>
科目:初中数学 来源: 题型:
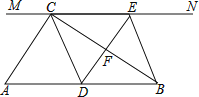
【题目】如图,在Rt△ABC中,![]() ,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明理由;
(3)若D为AB中点,则当![]() =______时,四边形BECD是正方形.
=______时,四边形BECD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点![]() .
.![]() .
.![]() ,完成系列问题:
,完成系列问题:
![]()
(1)将点![]() 向右移动六个单位长度到点
向右移动六个单位长度到点![]() ,在数轴上表示出点
,在数轴上表示出点![]() .
.
(2)在数轴上找到点![]() ,使点
,使点![]() 到
到![]() .
.![]() 两点的距离相等.并在数轴上标出点
两点的距离相等.并在数轴上标出点![]() 表示的数.
表示的数.
(3)在数轴上有一点![]() ,满足点
,满足点![]() 到点
到点![]() 与点
与点![]() 到点
到点![]() 的距离和是
的距离和是![]() ,则点
,则点![]() 表示的数是__________.
表示的数是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:我们知道,分数可分为“真分数”和“假分数”,而假分数都可化为带分数,如![]() 我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”,当分子的次数小于分母的次数时,我们称之为“真分式”,如
我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”,当分子的次数小于分母的次数时,我们称之为“真分式”,如![]() 这样的分式就是假分式;再如:
这样的分式就是假分式;再如:![]() 这样的分式就是真分式。类似的,假分式也可以化为带分式(即:整式与真分式的和的形式),如:
这样的分式就是真分式。类似的,假分式也可以化为带分式(即:整式与真分式的和的形式),如:
![]()
请解决下列问题:
(1)分式![]() 是_____分式(填“真”或“假”);
是_____分式(填“真”或“假”);
(2)将假分式![]() 化为带分式;
化为带分式;
(3)若分式![]() 的值为整数,直接写出所有符合条件的正整数
的值为整数,直接写出所有符合条件的正整数![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
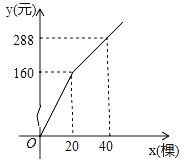
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com