
【题目】如图,已知一条直线过点![]() ,且与抛物线
,且与抛物线![]() 交于A、B两点,其中点A的横坐标是-2.
交于A、B两点,其中点A的横坐标是-2.
⑴求这条直线的函数关系式及点B的坐标 ;
⑵在![]() 轴上是否存在点C,使得ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在点C,使得ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
⑶.过线段AB上一点P,作PM∥![]() 轴,交抛物线于点M,点M在第一象限;点
轴,交抛物线于点M,点M在第一象限;点![]() ,当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
,当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?

【答案】(1)点B的坐标为(8,16);(2)点C的坐标为(![]() ,0),(0,0),(6,0),(32,0);(3)当M的横坐标为6时,MN+3PM的长度的最大值是18.
,0),(0,0),(6,0),(32,0);(3)当M的横坐标为6时,MN+3PM的长度的最大值是18.
【解析】试题分析:(1)、根据点A在二次函数上求出点A的坐标,然后利用待定系数法求出一次函数的解析式,根据一次函数和二次函数的交点坐标求出求出点B的坐标;(2)、根据点A和点B的坐标求出![]() 的值,设点C的坐标为(m,0),然后分别求出
的值,设点C的坐标为(m,0),然后分别求出![]() 和
和![]() 的值,然后根据勾股定理分三种情况进行讨论,分别求出m的值,得出点C的坐标;(3)、设点M的坐标为:(a,
的值,然后根据勾股定理分三种情况进行讨论,分别求出m的值,得出点C的坐标;(3)、设点M的坐标为:(a, ![]() ),MP与y轴交于点Q,根据Rt△MQN的勾股定理求出MN的长度,根据点P和点M的纵坐标相等得出点P的横坐标为
),MP与y轴交于点Q,根据Rt△MQN的勾股定理求出MN的长度,根据点P和点M的纵坐标相等得出点P的横坐标为![]() ,从而得出MN+3MP关于a的函数解析式,然后利用二次函数的性质得出最大值.
,从而得出MN+3MP关于a的函数解析式,然后利用二次函数的性质得出最大值.
试题解析:(1)、∵点A是直线与抛物线的交点,且横坐标为﹣2,
∴y=![]() ×(﹣2)2=1,A点的坐标为(﹣2,1),
×(﹣2)2=1,A点的坐标为(﹣2,1),
设直线的函数关系式为y=kx+b,
将(0,4),(﹣2,1)代入得: ![]() ,解得:
,解得: 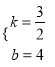 ,
,
∴直线y=![]() x+4, ∵直线与抛物线相交, ∴
x+4, ∵直线与抛物线相交, ∴![]() x+4=
x+4=![]() x2,解得:x=﹣2或x=8,
x2,解得:x=﹣2或x=8,
当x=8时,y=16, ∴点B的坐标为(8,16);
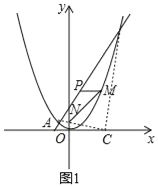
(2)、如图1,连接AC,BC, ∵由A(﹣2,1),B(8,16)可求得AB2=325.
设点C(m,0),同理可得AC2=(m+2)2+12=m2+4m+5, BC2=(m﹣8)2+162=m2﹣16m+320,
①若∠BAC=90°,则AB2+AC2=BC2,即325+m2+4m+5=m2﹣16m+320,解得:m=﹣![]() ;
;
②若∠ACB=90°,则AB2=AC2+BC2,即325=m2+4m+5+m2﹣16m+320, 解得:m=0或m=6;
③若∠ABC=90°,则AB2+BC2=AC2,即m2+4m+5=m2﹣16m+320+325, 解得:m=32;
∴点C的坐标为(﹣![]() ,0),(0,0),(6,0),(32,0)
,0),(0,0),(6,0),(32,0)
(3)设M(a, ![]() ),设MP与y轴交于点Q,
),设MP与y轴交于点Q,
在Rt△MQN中,由勾股定理得MN=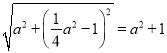 ,
,
又∵点P与点M纵坐标相同, ∴![]() +4=
+4=![]() , ∴x=
, ∴x=![]() , ∴点P的横坐标为
, ∴点P的横坐标为![]() ,
,
∴MP=a﹣![]() , ∴MN+3PM=
, ∴MN+3PM=![]() +1+3(a﹣
+1+3(a﹣![]() )=﹣
)=﹣![]() +3a+9,
+3a+9,
∴当a=﹣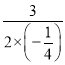 =6, 又∵﹣2≤6≤8, ∴取到最大值18,
=6, 又∵﹣2≤6≤8, ∴取到最大值18,
∴当M的横坐标为6时,MN+3PM的长度的最大值是18.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在等边三角形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的任意一点(点
边上的任意一点(点![]() 可以与点
可以与点![]() 重合,但不与点
重合,但不与点![]() 重合).过点
重合).过点![]() 作
作![]() ,垂足为
,垂足为![]() ;点
;点![]() 作
作![]() ,垂足为
,垂足为![]() ;过点
;过点![]() 作
作![]() ,垂足为
,垂足为![]() .设
.设![]() ,
,![]() .
.

(1)用含![]() 的代数式表示
的代数式表示![]() ,并注明
,并注明![]() 的取值范围;
的取值范围;
(2)当![]() 的长等于多少时,点
的长等于多少时,点![]() 和点
和点![]() 重合?
重合?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在八年级开展环保知识问卷调查活动,问卷一共10道题,八年级(三)班的问卷得分情况统计图如下图所示:

(1)扇形统计图中,![]() ______________;
______________;
(2)根据以上统计图中的信息,
①问卷得分的极差是_____________分;②问卷得分的众数是____________分;③问卷得分的中位数是______________分;
(3)请你求出该班同学的平均分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC,如图所示.
(1)求被剪掉阴影部分的面积:
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() .
.
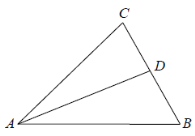
(1)尺规作图:作![]() 平分
平分![]() ,分别交
,分别交![]() 于点
于点![]() ;(保留作图痕迹,不必写出作法)
;(保留作图痕迹,不必写出作法)
(2)在(1)的条件下,求证:点![]() 在
在![]() 的平分线上;
的平分线上;
(3)若![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,请画出符合条件的图形,猜想
,请画出符合条件的图形,猜想![]() 和
和![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA=OB,AC=CD,已知两点A(4,0),C(0,7),点D在第一象限内,∠DCA=90°,点B在线段OC上,AB的延长线与DC的延长线交于点M,AC与BD交于点N.
(1)点B的坐标为: ;
(2)求点D的坐标;
(3)求证:CM=CN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】石狮泰禾某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售______ 件,每件盈利______ 元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲和乙同时从学校放学,两人以各自送度匀速步行回家,甲的家在学校的正西方向,乙的家在学校的正东方向,乙家离学校的距离比甲家离学校的距离远3900米,甲准备一回家就开始做什业,打开书包时发现错拿了乙的练习册.于是立即步去追乙,终于在途中追上了乙并交还了练习册,然后再以先前的速度步行回家,(甲在家中耽搁和交还作业的时间忽略不计)结果甲比乙晚回到家中,如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图,则甲的家和乙的家相距_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙3名学生各自随机选择到A、B 2个书店购书.
(1)求甲、乙2名学生在不同书店购书的概率;
(2)求甲、乙、丙3名学生在同一书店购书的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com