
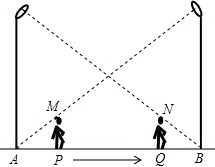
 如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.分析 (1)如图1,先证明△APM∽△ABD,利用相似比可得AP=$\frac{1}{6}$AB,再证明△BQN∽△BAC,利用相似比可得BQ=$\frac{1}{6}$AB,则$\frac{1}{6}$AB+12+AB=AB,解得AB=18(m);
(2)如图1,他在路灯A下的影子为BN,证明△NBM∽△NAC,利用相似三角形的性质得$\frac{BN}{BN+18}$=$\frac{1.6}{9.6}$,然后利用比例性质求出BN即可.
解答 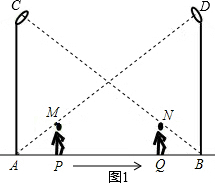 解:(1)如图1,
解:(1)如图1,
∵PM∥BD,
∴△APM∽△ABD,
$\frac{AP}{AB}$=$\frac{PM}{BD}$,即$\frac{AP}{AB}$=$\frac{1.6}{9.6}$,
∴AP=$\frac{1}{6}$AB,
∵NQ∥AC,
∴△BNQ∽△BCA,
∴$\frac{BQ}{BA}$=$\frac{QN}{AC}$,即$\frac{BQ}{AB}$=$\frac{1.6}{9.6}$,
∴BQ=$\frac{1}{6}$AB,
而AP+PQ+BQ=AB,
∴$\frac{1}{6}$AB+12+$\frac{1}{6}$AB=AB,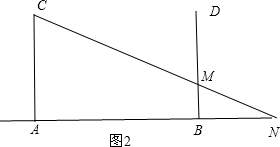
∴AB=18.
答:两路灯的距离为18m;
(2)如图1,他在路灯A下的影子为BN,
∵BM∥AC,
∴△NBM∽△NAC,
∴$\frac{BN}{AN}$=$\frac{BM}{AC}$,即$\frac{BN}{BN+18}$=$\frac{1.6}{9.6}$,解得BN=3.6.
答:当他走到路灯B时,他在路灯A下的影长是3.6m.
点评 本题考查了相似三角形的应用:通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
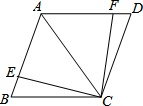 (1)如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF.求证:△ACE≌△ACF.
(1)如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF.求证:△ACE≌△ACF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com