
分析 根据点到原点的距离的定义即可求解;
分点在原点的左边与右边两种情况求解.
解答 解:数轴上表示-$\sqrt{6}$的点到原点的距离是$\sqrt{6}$,
①原点左边到原点的距离为4$\sqrt{2}$的点是-4$\sqrt{2}$;
②原点右边到原点的距离为4$\sqrt{2}$的点是4$\sqrt{2}$.
故到原点的距离为4$\sqrt{2}$的点表示的实数是-4$\sqrt{2}$或4$\sqrt{2}$.
故答案为:$\sqrt{6}$;-4$\sqrt{2}$或4$\sqrt{2}$.
点评 本题考查了实数与数轴,注意需要分点在原点的左右两边两种情况求解,避免漏解而导致出错.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:解答题
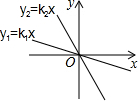 已知函数y=x;y=-2x.y=$\frac{1}{2}$x,y=3x.
已知函数y=x;y=-2x.y=$\frac{1}{2}$x,y=3x.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正整数、负整数统称整数 | B. | 正数、0、负数统称有理数 | ||
| C. | 开方开不尽的数和π统称无理数 | D. | 有理数、无理数统称实数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
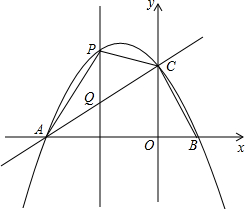 在平面直角坐标系中,抛物线y=-$\frac{1}{2}{x^2}$+bx+c的图象与x轴交于A、B两点,与y轴交于点C,已知A的坐标为(-3,0),tan∠CAB=$\frac{1}{2}$,直线x=m(-1≤m<0)交抛物线于点P,与直线AC交于点Q.
在平面直角坐标系中,抛物线y=-$\frac{1}{2}{x^2}$+bx+c的图象与x轴交于A、B两点,与y轴交于点C,已知A的坐标为(-3,0),tan∠CAB=$\frac{1}{2}$,直线x=m(-1≤m<0)交抛物线于点P,与直线AC交于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
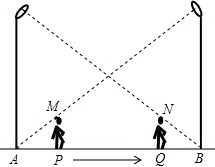 如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com