
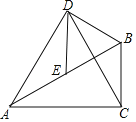
【题目】如图,在Rt△ABC中,(M2,N2),∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD,CD.
(1)求证:△ADE≌△CDB;
(2)若BC=![]() ,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
【答案】(1)证明见解析;(2)BH+EH的最小值为3.
【解析】
(1)只要证明△DEB是等边三角形,再根据SAS即可证明;
(2)如图,作点E关于直线AC点E',连接BE'交AC于点H.则点H即为符合条件的点.
(1)在Rt△ABC中,∠BAC=30°,E为AB边的中点,
∴BC=EA,∠ABC=60°,
∵△DEB为等边三角形,
∴DB=DE,∠DEB=∠DBE=60°,
∴∠DEA=120°,∠DBC=120°,
∴∠DEA=∠DBC,
∴△ADE≌△CDB;
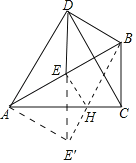
(2)如图,作点E关于直线AC点E',连接BE'交AC于点H,则点H即为符合条件的点,
由作图可知:EH=HE',AE'=AE,∠E'AC=∠BAC=30°,
∴∠EAE'=60°,
∴△EAE'为等边三角形,
∴E E'=EA=![]() AB,
AB,
∴∠AE'B=90°,
在Rt△ABC中,∠BAC=30°,BC=![]() ,
,
∴AB=2![]() ,A E'=AE=
,A E'=AE=![]() ,
,
∴B E'=![]() =3,
=3,
∴BH+EH的最小值为3.


科目:初中数学 来源: 题型:
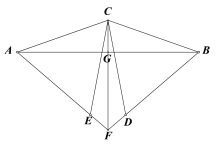
【题目】.如图所示,已知△ABC和△BDE都是等边三角形,下列结论:①AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°;⑤△BFG是等边三角形;⑥FG∥AD,其中正确的有( )

A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等腰三角形,AC=BC,△BDC和△ACE分别为等边三角形,直线AE与BD相交于点F,连接CF,交AB于点G.
(1)若∠ACB=150°,求∠AFB的度数;
(2)求证:AG=BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
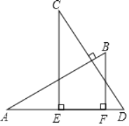
【题目】如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
A. a+cB. b+cC. a﹣b+cD. a+b﹣c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() )
)
例2 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() 或
或![]() 或
或![]() )
)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.
的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,![]() 的度数不同,得到
的度数不同,得到![]() 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形![]() 中,设
中,设![]() ,当
,当![]() 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠ACB=25°,现将ABCD沿EF折叠,使点C与点A重合,点D落在G处,则∠GFE的度数( ) 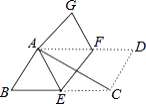
A.135°
B.120°
C.115°
D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形铁片ABCD的长为2a,宽为a; 为了要让铁片能穿过直径为 ![]() 的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔); 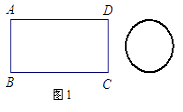
(1)如图2,M、N、P、Q分别是AD、AB、BC、CD的中点,若将矩形铁片的四个角去掉,只余下四边形MNPQ, ①则此时铁片是什么形状;
②给出证明,并通过计算说明此时铁片都能穿过圆孔;
(2)如图3,过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合),沿着这条直线将矩形铁片切割成两个全等的直角梯形铁片; 
①当BE=DF= ![]() 时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
②为了能使直角梯形铁片EBAF顺利穿过圆孔,请直接写出线段BE的长度的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
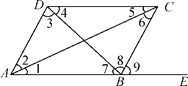
【题目】如图,(1)指出DC和AB被AC所截得的内错角;
(2)指出AD和BC被AE所截得的同位角;
(3)指出∠4与∠7,∠2与∠6,∠ADC与∠DAB各是什么关系的角,并指出各是哪两条直线被哪一条直线所截形成的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com