
【题目】某市自来水公司为限制单位用水,每月只给某单位计划内用水300吨,计划内用水每吨收费3. 4元,超计划部分每吨按4. 6元收费.
(1)用代数式表示(所填结果需化简):
设用水量为![]() 吨,当用水量小于等于300吨,需付款 元;当用水量大于300吨,需付款 元.
吨,当用水量小于等于300吨,需付款 元;当用水量大于300吨,需付款 元.
(2)若某单位4月份缴纳水费1480元,则该单位用水多少吨?
(3)若某单位5、6月份共用水750吨(6月份用水量超过5月份),共交水费2790元,则该单位5、6月份各用水多少吨?
【答案】(1)3.4x ,4.6x-360 ;(2)400;(3)5月用水250t,6月用水500t
【解析】
(1)根据收费标准,找出当x≤300及x>300两种情况下需付款数额;
(2)求出用水300吨时缴纳的水费,比较后可得出该单位4月份用水超过300吨,根据(1)的结论可得出关于x的一元一次方程,解之即可得出结论;
(3)设该单位5月份用水y吨,则6月份用水(700-y)吨,分y≤300及y>300两种情况考虑:①当y≤300时,根据(1)的结论可得出关于y的一元一次方程,解之即可得出结论;②当y>300时,由6月份用水量超过5月份可得出y的取值范围,再求出两个月的水费,比较后可得知该情况不成立.综上即可得出结论.
(1)当x≤300时,需付款3.4x元;
当x>300时,需付款300×3.4+4.6(x-300)=(4.6x-360)元.
故答案是:3.4x;(4.6x-360).
(2)∵3.4×300=1020(元),1020<1480,
∴该单位4月份用水超过300吨.
根据题意得:4.6x-360=1480,
解得:x=400.
答:该单位4月份用水400吨.
(3)设该单位5月份用水y吨,则6月份用水(750-y)吨.
①当y≤300时,有3.4y+4.6(750-y)-360=2790,
解得:y=250,
700-y=750-250=500;
②当y>300时,∵6月份用水量超过5月份,
∴750-y>y,
∴300<y<375.
∵600×3.4+(750-600)×4.6=2730≠2790,
∴此种情况不成立.
答:该单位5月份用水250吨,6月份用水500吨.


科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象如图,则下列说法:①
的图象如图,则下列说法:①![]() ;②
;② ![]() 是方程
是方程![]() 的解;③若点
的解;③若点![]() ,
,![]() 是这个函数的图象上的两点,且
是这个函数的图象上的两点,且![]() ,则
,则![]() ;④当
;④当![]() ,函数的值
,函数的值![]() ,则
,则![]() .其中正确的个数为( )
.其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于![]() 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过抛物线y= ![]() x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.
x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.
(1)求抛物线的对称轴和点B的坐标;
(2)在AB上任取一点P,连结OP,作点C关于直线OP的对称点D;
①连结BD,求BD的最小值;
②当点D落在抛物线的对称轴上,且在x轴上方时,求直线PD的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( ) ①试验条件不会影响某事件出现的频率;
②在相同的条件下试验次数越多,就越有可能得到较精确的估计值,但各人所得的值不一定相同;
③如果一枚骰子的质量分布均匀,那么抛掷后每个点数出现的机会均等;
④抛掷两枚质量分布均匀的相同的硬币,出现“两个正面”、“两个反面”、“一正一反”的机会相同.
A.①②
B.②③
C.③④
D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表记录了一名球员在罚球线上投篮的结果,
投篮次数(n) | 50 | 100 | 150 | 209 | 250 | 300 | 350 |
投中次数(m) | 28 | 60 | 78 | 104 | 123 | 152 | 175 |
投中频率(n/m) | 0.56 | 0.60 |
| 0.49 |
|
|
(1)计算并填写表中的投中频率(精确到0.01);
(2)这名球员投篮一次,投中的概率约是多少(精确到0.1)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:
单价x(元/件) | 30 | 34 | 38 | 40 | 42 |
销量y(件) | 40 | 32 | 24 | 20 | 16 |
(1)通过对上面表格中的数据进行分析,发现销量![]() (件)与单价
(件)与单价![]() (元/件)之间存在一次函数关系,求
(元/件)之间存在一次函数关系,求![]() 关于
关于![]() 的函数关系式(不需要写出函数自变量的取值范围);
的函数关系式(不需要写出函数自变量的取值范围);
(2)预计在今后的销售中,销量与单价仍然存在(1)中的关系,且该产品的成本是20元/件.为使工厂获得最大利润,该产品的单价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1.把△ABC分别绕直线AB和BC旋转一周,所得几何体的地面圆的周长分别记作l1 , l2 , 侧面积分别记作S1 , S2 , 则( )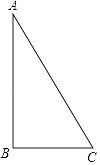
A.l1:l2=1:2,S1:S2=1:2
B.l1:l2=1:4,S1:S2=1:2
C.l1:l2=1:2,S1:S2=1:4
D.l1:l2=1:4,S1:S2=1:4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com