

分析 (1)根据直线MN与直线PQ垂直相交于O可知∠AOB=90°,再由AE、BE分别是∠BAO和∠ABO角的平分线得出∠BAE=$\frac{1}{2}$∠OAB,∠ABE=$\frac{1}{2}$∠ABO,由三角形内角和定理即可得出结论;
(2)延长AD、BC交于点F,根据直线MN与直线PQ垂直相交于O可得出∠AOB=90°,进而得出∠OAB+∠OBA=90°,故∠PAB+∠MBA=270°,再由AD、BC分别是∠BAP和∠ABM的角平分线,可知∠BAD=$\frac{1}{2}$∠BAP,∠ABC=$\frac{1}{2}$∠ABM,由三角形内角和定理可知∠F=45°,再根据DE、CE分别是∠ADC和∠BCD的角平分线可知∠CDE+∠DCE=112.5°,进而得出结论;
(3))由∠BAO与∠BOQ的角平分线相交于E可知∠EAO=$\frac{1}{2}$∠BAO,∠EOQ=$\frac{1}{2}$∠BOQ,进而得出∠E的度数,由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°,在△AEF中,由一个角是另一个角的3倍分四种情况进行分类讨论.
解答 解: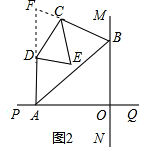 (1)∠AEB的大小不变,
(1)∠AEB的大小不变,
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴∠BAE=$\frac{1}{2}$∠OAB,∠ABE=$\frac{1}{2}$∠ABO,
∴∠BAE+∠ABE=$\frac{1}{2}$(∠OAB+∠ABO)=45°,
∴∠AEB=135°;
(2)∠CED的大小不变.
延长AD、BC交于点F.
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∴∠PAB+∠MBA=270°,
∵AD、BC分别是∠BAP和∠ABM的角平分线,
∴∠BAD=$\frac{1}{2}$∠BAP,∠ABC=$\frac{1}{2}$∠ABM,
∴∠BAD+∠ABC=$\frac{1}{2}$(∠PAB+∠ABM)=135°,
∴∠F=45°,
∴∠FDC+∠FCD=135°,
∴∠CDA+∠DCB=225°,
∵DE、CE分别是∠ADC和∠BCD的角平分线,
∴∠CDE+∠DCE=112.5°,
∴∠E=67.5°;
(3)∵∠BAO与∠BOQ的角平分线相交于E,
∴∠EAO=$\frac{1}{2}$∠BAO,∠EOQ=$\frac{1}{2}$∠BOQ,
∴∠E=∠EOQ-∠EAO=$\frac{1}{2}$(∠BOQ-∠BAO)=$\frac{1}{2}$∠ABO,
∵AE、AF分别是∠BAO和∠OAG的角平分线,
∴∠EAF=90°.
在△AEF中,∵有一个角是另一个角的3倍,故有:
①∠EAF=3∠E,∠E=30°,∠ABO=60°;
②∠EAF=3∠F,∠E=60°,∠ABO=120°(舍去);
③∠F=3∠E,∠E=22.5°,∠ABO=45°;
④∠E=3∠F,∠E=67.5°,∠ABO=135°(舍去).
∴∠ABO为60°或45°.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:选择题
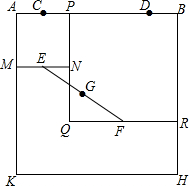 如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为( )
如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
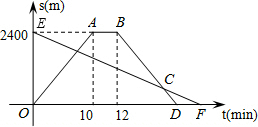 小华从家骑自行车出发,到相距2400米的银行办事,小华出发的同时,他哥哥以匀速的速度从银行沿同一条道路步行回家,小华在银行停留2分钟后沿原路以原速度返回,设他们出发后t分钟时,小华与家之间的距离为S1米,他哥与家之间的距离为S2米,如图中拆线OABD,线段EF分别是表示S1、S2与t之间函数关系的图象.
小华从家骑自行车出发,到相距2400米的银行办事,小华出发的同时,他哥哥以匀速的速度从银行沿同一条道路步行回家,小华在银行停留2分钟后沿原路以原速度返回,设他们出发后t分钟时,小华与家之间的距离为S1米,他哥与家之间的距离为S2米,如图中拆线OABD,线段EF分别是表示S1、S2与t之间函数关系的图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | x+1 | C. | $\frac{x+1}{x}$ | D. | $\frac{1}{x-1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com