
【题目】已知:如图,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且DE=BF.请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可).
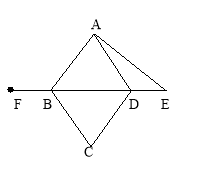
(1)连接 ;
(2)猜想: = ;
(3)证明:
【答案】(1)连结AF
(2)AF=AE
(3)证明:
∵四边形ABCD是菱形
∴AB=AD
∴∠ADB=∠ABD
∵∠ABD+∠ABF=180°
∠ADB+∠ADE=180°
∴∠ABF=∠ADE
∵BF = DE
∴△ABF≌△ADE(SAS)
∴AF=AE
【解析】
试题分析:根据观察图形,应该是连接AF或者CF
(1)连结AF(或连结CF)
(2)猜想AF=AE(连结CF的,则猜想CF=AE)
(3)证明:(以AF=AE为例,其他证法参照得分)
∵四边形ABCD是菱形
∴AB=AD
∴∠ADB=∠ABD
∵∠ABD+∠ABF=180°
∠ADB+∠ADE=180°
∴∠ABF=∠ADE
∵BF = DE
∴△ABF≌△ADE(SAS)
∴AF=AE


科目:初中数学 来源: 题型:
【题目】某公司研发1000件新产品,需要精加工后才能投放市场.现在甲、乙两个工厂加工这批产品,已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天,而乙工厂每天加工的件数是甲工厂每天加工件数的1.25倍,公司需付甲工厂加工费用每天100元,乙工厂加工费用每天125元.
(1)甲、乙两个工厂每天各能加工多少件新产品?
(2)两个工厂同时合作完成这批产品,共付加工费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°
得到△OA1B1 . 
(1)线段A1B1的长是 , ∠AOA1的度数是;
(2)连结AA1 , 求证:四边形OAA1B1是平行四边形;
(3)求四边形OAA1B1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)
(1)数轴上点B对应的数是______.
(2)经过几秒,点M、点N分别到原点O的距离相等?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内,△ABC和△ABD如图①放置,其中AB=BD.
小明做了如下操作:
将△ABC绕着边AC的中点旋转180°得到△CEA,将△ABD绕着边AD的中点旋转180°得到△DFA,如图②,请完成下列问题:
(1)试猜想四边形ABDF是什么特殊四边形,并说明理由;
(2)连接EF,CD,如图③,求证:四边形CDEF是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层,…,第n层.
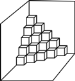
(1)第三层有________个小正方体;
(2)从第四层至第六层(含第四层和第六层)共有________个小正方体;
(3)第n层有________个小正方体;
(4)若每个小正方体边长为a分米,共摆放了n层,则要将摆放的小正方体能看到的表面部分涂上防锈漆,则防锈漆的总面积为________平方分米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
3﹣![]() =3×
=3×![]() ;
;
(﹣![]() )﹣6=(﹣
)﹣6=(﹣![]() )×6;
)×6;
(﹣0.5)﹣(﹣1)=(﹣0.5)×(﹣1)
根据上面这些等式反映的规律,解答下列问题:
(1)上面等式反映的规律用文字语言可以描述如下:存在两个有理数,使得这两个有理数的差等于
.
(2)若满足上述规律的两个有理数中有一个数是![]() ,求另一个有理数;
,求另一个有理数;
(3)若这两个有理数用字母a、b表示,则上面等式反映的规律用字母表示为 ;
(4)在(3)中的关系式中,字母a、b是否需要满足一定的条件?若需要,直接写出字母a、b应满足的条件;若不需要,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
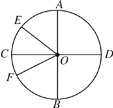
【题目】如图,圆O的直径为10 cm,两条直径AB,CD相交成90°角,∠AOE=50°,OF是∠BOE的平分线.
(1)求圆心角∠COF的度数;
(2)求扇形COF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com