
如图,已知抛物线y=x2+bx+c的顶点坐标为M(0,﹣1),与x轴交于A、B两点.
(1)求抛物线的解析式;
(2)判断△MAB的形状,并说明理由;
(3)过原点的任意直线(不与y轴重合)交抛物线于C、D两点,连接MC,MD,试判断MC、MD是否垂直,并说明理由.

(1)抛物线的解析式为:y=x2﹣1;
(2)△MAB是等腰直角三角形,理由见解析;
(3)MC⊥MF,理由见解析.
【解析】
试题分析:(1)待定系数法即可解得.
(2)由抛物线的解析式可知OA=OB=OC=1,得出∠AMO=∠MAO=∠BMO=∠BOM=45°从而得出△MAB是等腰直角三角形.
(3)分别过C点,D点作y轴的平行线,交x轴于E、F,过M点作x轴的平行线交EC于G,交DF于H,设D(m,m2﹣1),C(n,n2﹣1),通过FG∥DH,得出 ,从而求得m、n的关系,根据m、n的关系,得出△CGM∽△MHD,即可求得结论.
,从而求得m、n的关系,根据m、n的关系,得出△CGM∽△MHD,即可求得结论.
试题解析:(1)∵抛物线y=x2+bx+c的顶点坐标为M(0,﹣1),
∴b=0,c=﹣1,
∴抛物线的解析式为:y=x2﹣1;
(2)△MAB是等腰直角三角形,
由抛物线的解析式为:y=x2﹣1可知A(﹣1,0),B(1,0),
∴OA=OB=OC=1,
∴∠AMO=∠MAO=∠BMO=∠BOM=45°,
∴∠AMB=∠AMO+∠BMO=90°
∵y轴是对称轴,
∴A、B为对称点,
∴AM=BM,
∴△MAB是等腰直角三角形;
(3)MC⊥MF;分别过C点,D点作y轴的平行线,交x轴于E、F,过M点作x轴的平行线交EC于G,交DF于H,

设D(m,m2﹣1),C(n,n2﹣1),
∴OE=﹣n,CE=1﹣n2,OF=m,DF=m2﹣1,
∵OM=1,
∴CG=n2,DH=m2,
∵FG∥DH,
∴ ,
,
即
解得m=﹣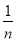 ,
,
又∵ =﹣n,
=﹣n, ,
,
∴ ,
,
∵∠CGM=∠MHD=90°,
∴△CGM∽△MHD,
∴∠CMG=∠MDH,
∵∠MDH+∠DMH=90°
∴∠CMG+∠DMH=90°,
∴∠CMD=90°,
即MC⊥MF.
考点:二次函数综合题.


科目:初中数学 来源:2014年初中毕业升学考试(四川甘孜卷)数学(解析版) 题型:解答题
如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y= 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
(1)求反比例函数解析式;
(2)求点C的坐标.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川德阳卷)数学(解析版) 题型:选择题
已知方程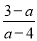 ﹣a=
﹣a=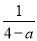 ,且关于x的不等式组
,且关于x的不等式组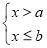 只有4个整数解,那么b的取值范围是( )
只有4个整数解,那么b的取值范围是( )
A.﹣1<b≤3 B.2<b≤3 C.8≤b<9 D.3≤b<4
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川德阳卷)数学(解析版) 题型:选择题
如图是某射击选手5次设计成绩的折线图,根据图示信息,这5次成绩的众数、中位数分别是( )

A.7、8 B.7、9 C.8、9 D.8、10
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川宜宾卷)数学(解析版) 题型:解答题
我市中小学全面开展“阳光体育”活动,某校在大课间中开设了A:体操,B:跑操,C:舞蹈,D:健美操四项活动,为了解学生最喜欢哪一项活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题:
(1)这次被调查的学生共有 人.
(2)请将统计图2补充完整.
(3)统计图1中B项目对应的扇形的圆心角是 度.
(4)已知该校共有学生3600人,请根据调查结果估计该校喜欢健美操的学生人数.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川南充卷)数学(解析版) 题型:解答题
已知关于x的一元二次方程x2-2 x+m=0,有两个不相等的实数根.
x+m=0,有两个不相等的实数根.
⑴求实数m的最大整数值;
⑵在⑴的条下,方程的实数根是x1,x2,求代数式x12+x22-x1x2的值.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川内江卷)数学(解析版) 题型:选择题
如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=2,则弦BC的长为( )

A. B.3 C.2
B.3 C.2 D.4
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com