
 如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式$\sqrt{a-2}$+(b-3)2=0,(c-4)2≤0
如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式$\sqrt{a-2}$+(b-3)2=0,(c-4)2≤0分析 (1)用非负数的性质求解;
(2)把四边形ABOP的面积看成两个三角形面积和,用m来表示;
(3)△ABC可求,是已知量,根据题意,方程即可.
解答 解:(1)由已知$\sqrt{a-2}$+(b-3)2=0,(c-4)2≤0
可得:a=2,b=3,c=4;
(2)∵S△ABO=$\frac{1}{2}$×2×3=3,S△APO=$\frac{1}{2}$×2×m=m,
∴S四边形ABOP=S△ABO+S△APO=3+m=3+m
(3)因为S△ABC=$\frac{1}{2}$×4×3=6,
∵S四边形ABOP=S△ABC
∴3+m=6,
则 m=3,
所以存在点P(-3,$\frac{1}{2}$)使S四边形ABOP=S△ABC.
点评 本题考查了坐标与图形性质及三角形的面积公式,关键根据题意画出图形,认真分析解答.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
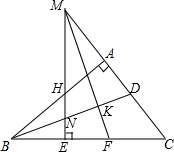 在△ABC中,∠BAC=90°,BD平分∠ABC,如图,M在CA的延长线上,ME⊥BC于E,ME分别交AB,BD于H,N,∠CME的平分线交BC于F,分别交AB,BD于G,K,求证:BD⊥MF.
在△ABC中,∠BAC=90°,BD平分∠ABC,如图,M在CA的延长线上,ME⊥BC于E,ME分别交AB,BD于H,N,∠CME的平分线交BC于F,分别交AB,BD于G,K,求证:BD⊥MF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组,并把解集在数轴上表示出来.
解不等式组,并把解集在数轴上表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
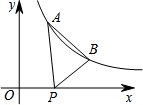 如图所示,已知A($\frac{1}{2}$,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$图象上的两点,动点P在x轴的非负半轴上运动,当线段AP与线段BP之差达到最大值时,点P的坐标是( )
如图所示,已知A($\frac{1}{2}$,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$图象上的两点,动点P在x轴的非负半轴上运动,当线段AP与线段BP之差达到最大值时,点P的坐标是( )| A. | $({\frac{5}{2},0})$ | B. | (3,0) | C. | $({\frac{7}{2},0})$ | D. | (4,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com