
【题目】(1)直线l1:y=x+1与x轴交于点A,直线l2:y=﹣x+3与x轴交于点B,l1与l2交于点C,直线l3过线段AB的中点和点C,求直线l3的解析式;
(2)已知平面直角坐标系中,直线l经过点P(2,1)且与双曲线y=![]() 交于A、B不同两点,问是否存在这样的直线l,使得点P恰好为线段AB的中点,若存在,求出直线l的解析式,若不存在,请说明理由;
交于A、B不同两点,问是否存在这样的直线l,使得点P恰好为线段AB的中点,若存在,求出直线l的解析式,若不存在,请说明理由;
(3)若A(x1,y1)、B(x2,y2)是抛物线y=4x2上的不同两点(y1≠y2),线段AB的垂直平分线与y轴交于点P,与线段AB交于点M(xm,ym),则称线段AB为点P的一条“相关弦”,若点P的坐标为(0,a)时(a为常数),证明点P的“相关弦”中点M的纵坐标相同.
【答案】(1)直线l3的表达式为:x=1;(2)直线l的表达式为:y=﹣![]() x+2,见解析;(3)见解析
x+2,见解析;(3)见解析
【解析】
(1)直线l1:y=x+1与x轴交于点A,直线l2:y=﹣x+3与x轴交于点B,则点A、B的坐标分别为:(﹣1,0)、(3,0),则AB 中点坐标为:(1,0),即可求解;
(2)直线l的表达式为:y=kx+1﹣2k,将直线l的表达式与反比例函数表达式联立并整理得:kx2+(1﹣2k)﹣3=0,则x1+x2=![]() =2,解得:k=﹣
=2,解得:k=﹣![]() ,;
,;
(3)设点A、B的坐标分别为:(m,4m2)、(n,4n2),则直线AB中垂线的表达式可设为:y=![]() x+a,点M的坐标为:(
x+a,点M的坐标为:(![]() ,
,![]() ),将点M的表达式代入AB中垂线的表达式得:yM=
),将点M的表达式代入AB中垂线的表达式得:yM=![]() =
=![]() ×
×![]() +a=
+a=![]() +a.
+a.
解:(1)直线l1:y=x+1与x轴交于点A,直线l2:y=﹣x+3与x轴交于点B,
则点A、B的坐标分别为:(﹣1,0)、(3,0),则AB 中点坐标为:(1,0),
联立l1、l2的表达式并解得:x=1,故点C(1,2),
故直线l3的表达式为:x=1;
(2)设直线l的表达式为:y=kx+b,将点P的坐标代入上式并解得:
直线l的表达式为:y=kx+1﹣2k,
将直线l的表达式与反比例函数表达式联立并整理得:kx2+(1﹣2k)﹣3=0,
则x1+x2=![]() =2,解得:k=﹣
=2,解得:k=﹣![]() ,
,
故直线l的表达式为:y=﹣![]() x+2;
x+2;
(3)设点A、B的坐标分别为:(m,4m2)、(n,4n2),
则直线AB表达式中的k值为:![]() =4m+4n,
=4m+4n,
则直线AB中垂线的表达式可设为:y=![]() x+a,
x+a,
点M的坐标为:(![]() ,
,![]() ),
),
将点M的表达式代入AB中垂线的表达式得:yM=![]() ,
,
故点P的“相关弦”中点M的纵坐标为常数,即都相同.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (k≠0,x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,E(
(k≠0,x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,E(![]() ,6),且E为BC的中点,D为x轴负半轴上的点.
,6),且E为BC的中点,D为x轴负半轴上的点.

(1)求反比倒函数的表达式和点F的坐标;
(2)若D(﹣![]() ,0),连接DE、DF、EF,则△DEF的面积是 .
,0),连接DE、DF、EF,则△DEF的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方方驾驶小汽车匀速地从A地行使到B地,行驶里程为480千米,设小汽车的行使时间为t(单位:小时),行使速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.
⑴求v关于t的函数表达式;
⑵方方上午8点驾驶小汽车从A出发.
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围.
②方方能否在当天11点30分前到达B地?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品用甲种原料9千克,乙种原料3千克,可获利700元;生产一件B种产品用甲种原料4千克,乙种原料10千克,可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润为y元,其中一种产品生产件数为x件,试写出y与x之间的函数关系式,并利用函数的性质说明那种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,ABCD中,E、F分别是边AB、CD的中点.
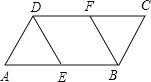
(1)求证:四边形EBFD是平行四边形;
(2)若AD=AE=2,∠A=60°,求四边形EBFD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax![]() +bx+c的图象如图所示,下列结论:①abc>0;②b<a+c;③4a+2b+c>0;④a+b+c>m(am+b)+c(m≠1的实数),其中正确的结论有 ( )
+bx+c的图象如图所示,下列结论:①abc>0;②b<a+c;③4a+2b+c>0;④a+b+c>m(am+b)+c(m≠1的实数),其中正确的结论有 ( )
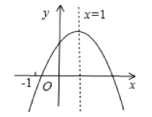
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D为AC中点,E为AB上的动点,将ED绕点D逆时针旋转90°得到FD,连CF,则线段CF的最小值为_____.
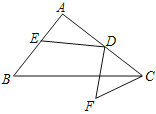
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有若干个除颜色外其余均相同的红、黄、蓝三种颜色的小球,其中红球2个,篮球1个,若从中任意摸出一个球,摸到球是红球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,求两次摸到球的颜色是红色与黄色这种组合(不考虑红、黄球顺序)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com