
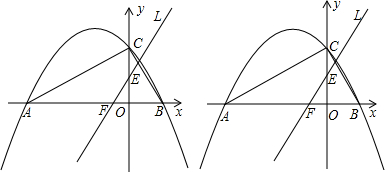
���� ��1����ͼ1������AC����Rt��AOC�У���CAB=30�㣬�������Ǻ����ɵ�C��0��$\sqrt{3}$�������ݴ���ϵ�������������߽���ʽ��
��2�����������֪��OE=m��OD=$\frac{\sqrt{3}}{3}$m����DEO=30�㣬���ݵ���ֱ�������ε��ж������ʷ����������
��i����ͼ2����PD��DE��DP=DE����PQ��x�
��ii����ͼ3����PE��DE��PE=DE����PQ��y���iii����ͼ4����DP��DE��DP=PE����DM��AC��EN��AC���������ۿ����P�����ꣻ
�ڶ�ֱ��l��ֱ��AC�Ľ���ΪC�Ͷ�ֱ��l��y��Ľ�����x�����棬������ǰ���ֱ��ƽ�У�����m��ȡֵ��Χ��
��� �⣺��1����ͼ1������AC����Rt��AOC�У���CAB=30�㣬
��A��-3��0������OA=3��
��OC=$\sqrt{3}$����C��0��$\sqrt{3}$����
�������߽���ʽΪy=ax2+bx+$\sqrt{3}$��
��A��-3��0����B��1��0������� $\left\{\begin{array}{l}{a+b+\sqrt{3}=0}\\{9a-3b+c=0}\end{array}\right.$��
��� $\left\{\begin{array}{l}{a=-\frac{\sqrt{3}}{3}}\\{b=-\frac{2\sqrt{3}}{3}}\end{array}\right.$��
��y=-$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x+$\sqrt{3}$��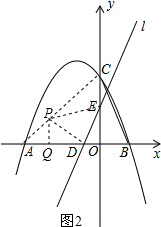 ��2���������֪��OE=m��OD=$\frac{\sqrt{3}}{3}$m����DEO=30�㣬
��2���������֪��OE=m��OD=$\frac{\sqrt{3}}{3}$m����DEO=30�㣬
��i����ͼ2����PD��DE��DP=DE����PQ��x��
���PQD=��EOD=90�㣬
��PDQ+��EDO=90�㣬��EDO+��DEO=90�㣬
���DEO=��PDQ=30�㣬
�ڡ�DPQ���EDO�У�
$\left\{\begin{array}{l}{��PQD=��EOD}\\{��DEO=��PDQ}\\{DP=DE}\end{array}\right.$��
���DPQ�ա�EDO��AAS����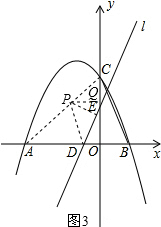 ��DQ=OE=m��
��DQ=OE=m��
�ߡ�PAQ=��PDQ=30�㣬
��PA=PD��
��AQ=DQ=m��
��OA=2m+$\frac{\sqrt{3}}{3}$m=3��
��m=$\frac{9}{6+\sqrt{3}}$=$\frac{18-3\sqrt{3}}{11}$��
��ii����ͼ3����PE��DE��PE=DE����PQ��y�ᣬ
ͬ���ɵ�CQ=EQ=OD=$\frac{\sqrt{3}}{3}$m��
��OC=m+$\frac{2\sqrt{3}}{3}$m=$\sqrt{3}$��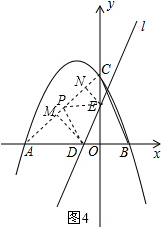 ��m=$\frac{9-3\sqrt{3}}{3+\sqrt{3}}$=6-3$\sqrt{3}$��
��m=$\frac{9-3\sqrt{3}}{3+\sqrt{3}}$=6-3$\sqrt{3}$��
��iii����ͼ4����DP��DE��DP=PE����DM��AC��EN��AC��
ͬ���ɵ�AP=AD=$\frac{9-\sqrt{3}m}{3}$��PN=DM=$\frac{9-\sqrt{3}m}{6}$��CN=$\frac{\sqrt{3}-m}{2}$��
��AC=$\frac{9-\sqrt{3}m}{3}$+$\frac{9-\sqrt{3}m}{6}$+$\frac{\sqrt{3}-m}{2}$=2$\sqrt{3}$��
��m=$\frac{9-3\sqrt{3}}{\sqrt{3}+1}$=6$\sqrt{3}$-9��
�ڵ�x=0��y=$\sqrt{3}$ʱ��$\sqrt{3}$=0+m�����m=$\sqrt{3}$��
��x=0��y=-$\frac{\sqrt{3}}{3}$ʱ��-$\frac{\sqrt{3}}{3}$=0+m�����m=-$\frac{\sqrt{3}}{3}$��
��m��ȡֵ��ΧΪ��-$\frac{\sqrt{3}}{3}$��m��$\sqrt{3}$��
���� ���⿼���˶��κ����ۺ��⣬�漰��֪ʶ���У����Ǻ���������ϵ�����������߽���ʽ������ֱ�������ε��ж������ʣ�ȫ�������ε��ж������ʣ�����˼������ã���ԳƵ����ʣ��ۺ��Խ�ǿ����һ�����Ѷȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�AB=AC=10��sinB=$\frac{3}{5}$��
��ͼ���ڡ�ABC�У�AB=AC=10��sinB=$\frac{3}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
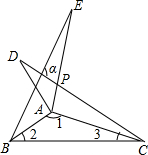 ��ͼ����ABE����ADC�͡�ABC�ֱ��ǹ���AB��AC������ֱ�ߵ���Գ�ͼ�Σ�����1����2����3=7��2��1����Ϧ��Ķ���Ϊ108�㣮
��ͼ����ABE����ADC�͡�ABC�ֱ��ǹ���AB��AC������ֱ�ߵ���Գ�ͼ�Σ�����1����2����3=7��2��1����Ϧ��Ķ���Ϊ108�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
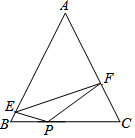 ��֪����ͼ���ڡ�ABC�У�AB=AC��tanA=$\frac{4}{3}$��PΪBC��һ�㣬��BP��PC=3��5��E��F�ֱ�ΪAB��AC�ϵĵ㣬�ҡ�EPF=2��B������EPF�����Ϊ6����EF=2$\sqrt{13}$��
��֪����ͼ���ڡ�ABC�У�AB=AC��tanA=$\frac{4}{3}$��PΪBC��һ�㣬��BP��PC=3��5��E��F�ֱ�ΪAB��AC�ϵĵ㣬�ҡ�EPF=2��B������EPF�����Ϊ6����EF=2$\sqrt{13}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
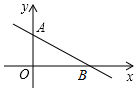 ƽ��ֱ������ϵ�У�ֱ��y=-$\frac{1}{2}$x+2��x��y�ύ��A��B���㣬�ڵڶ���������һ��P��ʹ��PAO�͡�AOB���Ƶ������θ���Ϊ��������
ƽ��ֱ������ϵ�У�ֱ��y=-$\frac{1}{2}$x+2��x��y�ύ��A��B���㣬�ڵڶ���������һ��P��ʹ��PAO�͡�AOB���Ƶ������θ���Ϊ��������| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com