
【题目】如图AC是⊙O的直径,PA切⊙O于点A,点B是⊙O上的一点,且∠BAC=30°,
∠APB=60°.
(1)求证:PB是⊙O的切线;
(2)若⊙O的半径为2,求PA及弦AB长.

【答案】(1)证明见解析;(2)PA=2![]() ,AB=2
,AB=2![]()
【解析】(1)证明:连接OB.
∵OA=OB,∴∠OBA=∠BAC=30°
∴∠AOB=180°-30°-30°=120°
∵PA切⊙O于点A,
∴OA⊥PA,即∠OAP=90°.
∵四边形的内角和为360°,
∴∠OBP=360°-90°-60°-120°=90°.
∴OB⊥PB.
又∵点B是⊙O上的一点,
∴PB是⊙O的切线.
(2)解:连接OP.∵PA、PB是⊙O的切线,∴PA=PB,∠OPA=
∠OPB=![]() ∠APB=30°.
∠APB=30°.
在Rt△OAP中,∠OAP=90°,∠OPA=30°
∴OP=2OA=2×2=4,
∴PA=![]() =
=![]() =2
=2![]()
∵PA=PB,∠APB=60°,∴PA=PB=AB=2![]()


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线y=mx+n与反比例函数![]() 交于A、B两点,点A在点B的左边,与x轴、y轴分别交于点C、点D,AE⊥x轴于E,BF⊥y轴于F
交于A、B两点,点A在点B的左边,与x轴、y轴分别交于点C、点D,AE⊥x轴于E,BF⊥y轴于F
(1)直接写出m、n、k的正负性
(2) 若m=1,n=3,k=4,求直线EF的解析式
(3)写出AC、BD的数量关系,并证明

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母A,B,C依次表示这三个诵读材料),将A,B,C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小明和小亮参加诵读比赛,比赛时小明先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
(1)小明诵读《论语》的概率是 .
(2)请用列表法或画树状图法求小明和小亮诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,求证:DE=BD+CE. 
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明:若不成立,请说明理由. 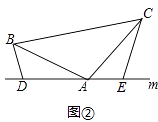
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+2 ![]() 与x、y轴分别交于A、B两点,以OB为边在y轴左侧作等边△OBC,将△OBC沿y轴上下平移,使点C的对应点C′恰好落在直线AB上,则点C'的坐标为 .
与x、y轴分别交于A、B两点,以OB为边在y轴左侧作等边△OBC,将△OBC沿y轴上下平移,使点C的对应点C′恰好落在直线AB上,则点C'的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中①过一点有且只有一条直线与已知直线平行;②在同一平面内,过一点有且只有一条直线与已知直线垂直;③两直线平行,同旁内角互补;④直线外一点到已知直线的垂线段就是点到直线的距离,其中正确的有( )个
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com