
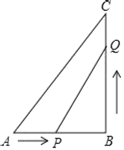
【题目】已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发.
(1)几秒后,△PBQ的面积等于6cm2?
(2)几秒后,四边形APQC的面积最小?最小值是多少?
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
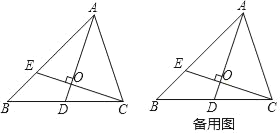
【题目】如图,△ABC中,D是边BC的中点,E是AB边上一点,且AD⊥CE于O,AD=AC=CE.
(1)求证:∠B=45°;
(2)求![]() 的值;
的值;
(3)直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
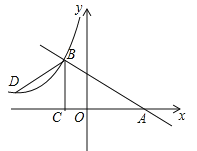
【题目】如图,已知一次函数y=kx+b的图象与x轴交于点A,与反比例函数![]() (x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(1)求m的值;
(2)若∠DBC=∠ABC,求一次函数y=kx+b的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市拟于中秋节前![]() 天里销售某品牌月饼,其进价为
天里销售某品牌月饼,其进价为![]() 元/
元/![]() .设第
.设第![]() 天的销售价格为
天的销售价格为![]() (元/
(元/![]() ),销售量为
),销售量为![]() .该超市根据以往的销售经验得出以下的销售规律:①当
.该超市根据以往的销售经验得出以下的销售规律:①当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 与
与![]() 满足一次函数关系,且当
满足一次函数关系,且当![]() 时,
时,![]() ;
;![]() 时,
时,![]() .②
.②![]() 与
与![]() 的关系为
的关系为![]() .
.
(1)当![]() 时,
时,![]() 与
与![]() 的关系式为 ;
的关系式为 ;
(2)![]() 为多少时,当天的销售利润
为多少时,当天的销售利润![]() (元)最大?最大利润为多少?
(元)最大?最大利润为多少?
(3)若超市希望第![]() 天到第
天到第![]() 天的日销售利润
天的日销售利润![]() (元)随
(元)随![]() 的增大而增大,则需要在当天销售价格的基础上涨
的增大而增大,则需要在当天销售价格的基础上涨![]() 元/
元/![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台州人民翘首以盼的乐清湾大桥于2018年9月28日正式通车,经统计分析,大桥上的车流速度![]() (千米/小时)是车流密度
(千米/小时)是车流密度![]() (辆/千米)的函数,当桥上的车流密度达到220辆/千米的时候就造成交通堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米,车流速度为80千米/小时,研究证明:当
(辆/千米)的函数,当桥上的车流密度达到220辆/千米的时候就造成交通堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米,车流速度为80千米/小时,研究证明:当![]() 时,车流速度
时,车流速度![]() 是车流密度
是车流密度![]() 的一次函数.
的一次函数.
(1)求大桥上车流密度为50/辆千米时的车流速度;
(2)在某一交通高峰时段,为使大桥上的车流速度大于60千米/小时且小于80千米/小时,应把大桥上的车流密度控制在什么范围内?
(3)车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量![]() 车流速度
车流速度![]() 车流密度,求大桥上车流量
车流密度,求大桥上车流量![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若数a使关于x的不等式组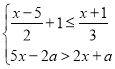 至少有3个整数解,且使关于y的分式方程
至少有3个整数解,且使关于y的分式方程![]() =2有非负整数解,则满足条件的所有整数a的和是( )
=2有非负整数解,则满足条件的所有整数a的和是( )
A. 14B. 15C. 23D. 24
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com