
����Ŀ��ij�������������ǰ![]() ��������ijƷ���±��������Ϊ
��������ijƷ���±��������Ϊ![]() Ԫ/
Ԫ/![]() �����
�����![]() ������ۼ۸�Ϊ
������ۼ۸�Ϊ![]() ��Ԫ/
��Ԫ/![]() ����������Ϊ
����������Ϊ![]() ���ó��и������������۾���ó����µ����۹��ɣ��ٵ�
���ó��и������������۾���ó����µ����۹��ɣ��ٵ�![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ��
��![]() ����һ�κ�����ϵ���ҵ�
����һ�κ�����ϵ���ҵ�![]() ʱ��
ʱ��![]() ��
��![]() ʱ��
ʱ��![]() ����
����![]() ��
��![]() �Ĺ�ϵΪ
�Ĺ�ϵΪ![]() ��
��
��1����![]() ʱ��
ʱ��![]() ��
��![]() �Ĺ�ϵʽΪ�� ����
�Ĺ�ϵʽΪ�� ����
��2��![]() Ϊ����ʱ���������������
Ϊ����ʱ���������������![]() ��Ԫ������������Ϊ���٣�
��Ԫ������������Ϊ���٣�
��3��������ϣ����![]() �쵽��
�쵽��![]() �������������
�������������![]() ��Ԫ����
��Ԫ����![]() ���������������Ҫ�ڵ������ۼ۸�Ļ�������
���������������Ҫ�ڵ������ۼ۸�Ļ�������![]() Ԫ/
Ԫ/![]() ����
����![]() ����Сֵ��
����Сֵ��
���𰸡���1��![]() ����2��
����2��![]() Ϊ
Ϊ![]() ʱ���������������
ʱ���������������![]() ��Ԫ������������Ϊ
��Ԫ������������Ϊ![]() Ԫ����3��3
Ԫ����3��3
��������
��1�������������ô���ϵ�������ó���![]() ʱ��
ʱ��![]() ��
��![]() �Ĺ�ϵʽΪ��
�Ĺ�ϵʽΪ��![]() ��
��
��2�������������������������ۼ۩����ۣ����г�ÿ�����������![]() ��Ԫ�������ۼ�
��Ԫ�������ۼ�![]() ��Ԫ/�䣩֮��ĺ�����ϵʽ�������ݺ���������������������
��Ԫ/�䣩֮��ĺ�����ϵʽ�������ݺ���������������������
��3��Ҫʹ��![]() �쵽��
�쵽��![]() �������������
�������������![]() ��Ԫ����
��Ԫ����![]() �������������Գ���
�������������Գ���![]() �����
�����![]() ����
����
��1�������⣬��![]() ʱ��
ʱ��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ����
ʱ����![]() ��
��
����![]() �����
�����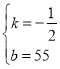
![]() ��
��![]() �Ĺ�ϵʽΪ��
�Ĺ�ϵʽΪ��![]()
��2�������⣬
![]()
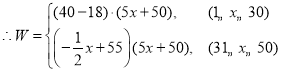
�����ã� 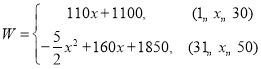
��![]() ʱ��
ʱ��
![]() ��
��![]() ���������
���������
![]() ʱ��ȡ���ֵ
ʱ��ȡ���ֵ![]()
��![]() ʱ��
ʱ��
![]()
![]()
![]() ʱ��
ʱ��![]() ȡ�����ֵ����ʱ
ȡ�����ֵ����ʱ![]()
����������![]() Ϊ
Ϊ![]() ʱ���������������
ʱ���������������![]() ��Ԫ������������Ϊ
��Ԫ������������Ϊ![]() Ԫ
Ԫ
��3�������⣬
![]()
![]()
![]() ��
��![]() �쵽��
�쵽��![]() �������������
�������������![]() ��Ԫ����
��Ԫ����![]() �����������
�����������
![]() �Գ���
�Գ���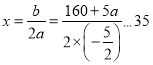 ����
����![]()
��![]() ����СֵΪ
����СֵΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��![]() +1�������ʣ���������������һ�㵽����F��0��2���ľ����뵽��ľ���ʼ����ȣ���ͼ����M������Ϊ��
+1�������ʣ���������������һ�㵽����F��0��2���ľ����뵽��ľ���ʼ����ȣ���ͼ����M������Ϊ��![]() ��3����P��������y��
��3����P��������y��![]() +1��һ�����㣬���PMF�ܳ�����Сֵ��_____��
+1��һ�����㣬���PMF�ܳ�����Сֵ��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
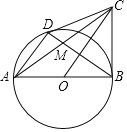
����Ŀ����ͼ����֪AB�ǡ�O��ֱ����CB��AB��DΪԲ��һ�㣬��AD��OC������CD��AC��BD��AC��BD���ڵ�M��
��1����֤��CDΪ��O�����ߣ�
��2����CD��![]() AD����
AD����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD���ܳ���48cm�� AE��BC������ΪE��AF��CD������ΪF����EAF��2��C��
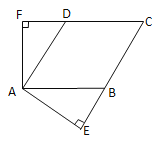
��1�����C�Ķ�����
��2����֪DF�ij��ǹ���x�ķ���x2��5x��a��0��һ��������÷��̵���һ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������ţ���������ˮ��2mʱ��ˮ���4m��ˮ���½�2m��ˮ���������______m.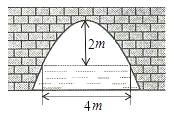
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��B�����ڲ�����A���������ĸ����������ȫ��ͬ��С��С���Ϸֱ��������0��1��2��3��B���������������������ȫ��ͬ��С��С���Ϸֱ��������0��1��2��С���ȴ�A���������ȡ��һ��С����m��ʾȡ�������ϱ��е����֣��ٴ�B���������ȡ��һ��С����n��ʾȡ�������ϱ��е����֣�
��1�����ã�m��n����ʾС��ȡ��ʱm��n �Ķ�Ӧֵ���뻭����״ͼ��д����m��n��������ȡֵ��
��2�������x��һԪ���η���![]() ��ʵ�����ĸ��ʣ�
��ʵ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
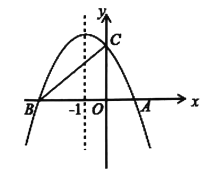
����Ŀ����ͼ�����κ���![]() ��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C����A������Ϊ(2��0)����C������Ϊ(0��4)�����ĶԳ�����ֱ��x=-1.
��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C����A������Ϊ(2��0)����C������Ϊ(0��4)�����ĶԳ�����ֱ��x=-1.
(1)��������κ����Ľ���ʽ��
(2)�ڵڶ����������������Ƿ����һ��P��ʹ![]() �������������ڣ����
�������������ڣ����![]() ��������ֵ����û�У���˵������.
��������ֵ����û�У���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�������Σ�����AC����![]() �Ƶ�A��ʱ����ת����
�Ƶ�A��ʱ����ת����![]() ������CF��OΪCF���е㣬����OE��OD��
������CF��OΪCF���е㣬����OE��OD��
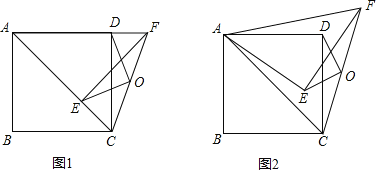
��1����ͼ1����![]() ʱ����ֱ��д��OE��OD�Ĺ�ϵ������֤������
ʱ����ֱ��д��OE��OD�Ĺ�ϵ������֤������
��2����ͼ2����![]() ʱ����1���еĽ����Ƿ��������˵�����ɣ�
ʱ����1���еĽ����Ƿ��������˵�����ɣ�
��3����![]() ʱ����
ʱ����![]() ����ֱ��д����O������·������
����ֱ��д����O������·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ���й�������Ϊ30Ԫ��ͯװ���ɼ�����۲��Ź涨�����۵��۲�����ÿ��30Ԫ��������ÿ��60Ԫ������һ��ʱ����֣������۵���Ϊ60Ԫʱ��ƽ��ÿ��������Ϊ80�����������۵���ÿ����10Ԫʱ��ƽ��ÿ���ܶ��۳�20����ͬʱ�������۹����У�ÿ�»�Ҫ֧����������450Ԫ�������۵���ΪxԪ��ƽ����������Ϊy����
��1�����y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2�������۵���Ϊ����Ԫʱ����������ͯװÿ�¿ɻ���1800Ԫ��
��3�������۵���Ϊ����Ԫʱ����������ͯװÿ�»�����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com