
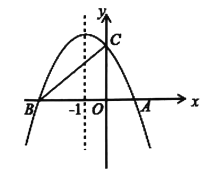
【题目】如图,二次函数![]() 的图象与x轴交于A、B两点,与y轴交于点C,点A的坐标为(2,0),点C的坐标为(0,4),它的对称轴是直线x=-1.
的图象与x轴交于A、B两点,与y轴交于点C,点A的坐标为(2,0),点C的坐标为(0,4),它的对称轴是直线x=-1.
(1)求这个二次函数的解析式;
(2)在第二象限内抛物线上是否存在一点P,使![]() 的面积最大?若存在,求出
的面积最大?若存在,求出![]() 的面积最大值;若没有,请说明理由.
的面积最大值;若没有,请说明理由.
【答案】(1)![]() ;(2)x=-2时,△PBC的面积最大为4.
;(2)x=-2时,△PBC的面积最大为4.
【解析】
(1)利用待定系数法求出即可得出结论;
(2)根据A点坐标及对称轴求出B点坐标,设P点(x,![]() )(-4<x<0),求出S△BPC=-(x+2)2+4,即可求出最大值.
)(-4<x<0),求出S△BPC=-(x+2)2+4,即可求出最大值.
解:(1)根据题意得,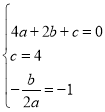 ,
,
解得: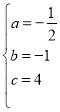 ,
,
∴二次函数的解析式![]() ;
;
(2)如图,存在.

理由如下:
∵A的坐标为(2,0),它的对称轴是直线x=-1.
∴点B的坐标为(-4,0),
设P点(x,![]() )(-4<x<0),
)(-4<x<0),
∵S△BPC=S四边形BPCO-S△BOC
=S△BOP+S△COP-S△BOC
=![]() ×4×(
×4×(![]() )+
)+![]() ×4×(-x)-
×4×(-x)- ![]() ×4×4
×4×4
=-x2-4x
=-(x+2)2+4,
∴x=-2时,△PBC的面积最大为4.


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
【题目】在甲乙两个不透明的口袋中,分别有大小、材质完全相同的小球,其中甲口袋中的小球上分别标有数字1,2,3,4,乙口袋中的小球上分别标有数字2,3,4,先从甲袋中任意摸出一个小球,记下数字为m,再从乙袋中摸出一个小球,记下数字为n.
(1)请用列表或画树状图的方法表示出所有(m,n)可能的结果;
(2)若m,n都是方程x2﹣5x+6=0的解时,则小明获胜;若m,n都不是方程x2﹣5x+6=0的解时,则小利获胜,问他们两人谁获胜的概率大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年中国北京世界园艺博览会(以下简称“世园会”)于4月29日至10月7日在北京延庆区举行.世园会为满足大家的游览需求,倾情打造了4条各具特色的趣玩路线,分别是:![]() .“解密世园会”、
.“解密世园会”、![]() .“爱我家,爱园艺”、
.“爱我家,爱园艺”、![]() .“园艺小清新之旅”和
.“园艺小清新之旅”和![]() .“快速车览之旅”.李欣和张帆都计划暑假去世园会,他们各自在这4条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
.“快速车览之旅”.李欣和张帆都计划暑假去世园会,他们各自在这4条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
(1)李欣选择线路![]() .“园艺小清新之旅”的概率是多少?
.“园艺小清新之旅”的概率是多少?
(2)用画树状图或列表的方法,求李欣和张帆恰好选择同一线路游览的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市拟于中秋节前![]() 天里销售某品牌月饼,其进价为
天里销售某品牌月饼,其进价为![]() 元/
元/![]() .设第
.设第![]() 天的销售价格为
天的销售价格为![]() (元/
(元/![]() ),销售量为
),销售量为![]() .该超市根据以往的销售经验得出以下的销售规律:①当
.该超市根据以往的销售经验得出以下的销售规律:①当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 与
与![]() 满足一次函数关系,且当
满足一次函数关系,且当![]() 时,
时,![]() ;
;![]() 时,
时,![]() .②
.②![]() 与
与![]() 的关系为
的关系为![]() .
.
(1)当![]() 时,
时,![]() 与
与![]() 的关系式为 ;
的关系式为 ;
(2)![]() 为多少时,当天的销售利润
为多少时,当天的销售利润![]() (元)最大?最大利润为多少?
(元)最大?最大利润为多少?
(3)若超市希望第![]() 天到第
天到第![]() 天的日销售利润
天的日销售利润![]() (元)随
(元)随![]() 的增大而增大,则需要在当天销售价格的基础上涨
的增大而增大,则需要在当天销售价格的基础上涨![]() 元/
元/![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一抛物线的对称轴为直线![]() ,与y轴负半轴交于C点,与x轴交于A、B两点,其中B点的坐标为(3,0),且OB=OC.
,与y轴负半轴交于C点,与x轴交于A、B两点,其中B点的坐标为(3,0),且OB=OC.
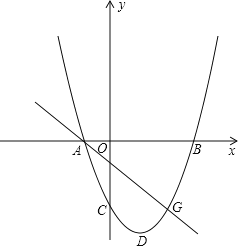
(1)求此抛物线的解析式;
(2)若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.
(3)若平行于x轴的直线与该抛物线交于M、N两点(其中点M在点N的右侧),在x轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一路灯距地面6.4米,身高1.6米的小方从距离灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增长3米,
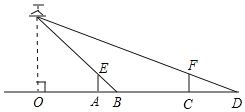
求:(1)小方在A处时的影子AB的长;(2)小方行走的路程AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将矩形纸片ABCD折叠,使得顶点A与边CD上的动点P重合(点P不与点C、D重合),MN为折痕,点M、N分别在边BC、AD上,连结AM、MP、AP,其中,AP与MN相交于点F.⊙O过点M、C、P
(1)若∠AMP=90°,求证:BM=CP;
(2)随着点P的运动,若⊙O与AM相切于点M,又与AD相切于点H,且AB=4,求CP的长.
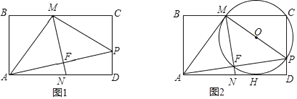
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,则DM的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com