
【题目】如图所示,将矩形纸片ABCD折叠,使得顶点A与边CD上的动点P重合(点P不与点C、D重合),MN为折痕,点M、N分别在边BC、AD上,连结AM、MP、AP,其中,AP与MN相交于点F.⊙O过点M、C、P
(1)若∠AMP=90°,求证:BM=CP;
(2)随着点P的运动,若⊙O与AM相切于点M,又与AD相切于点H,且AB=4,求CP的长.
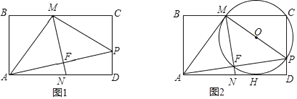
【答案】(1)证明见解析;(2)3.
【解析】
(1)由矩形的性质得出∠B=∠C=90°,证出∠BAM=∠CMP,由折叠的性质得出AM=PM,由AAS证明△ABM≌△MPC,即可得出结论;
(2)连接HO并延长交BC于J,根据折叠的性质知:MN垂直平分AP,可得:AM=PM,AM为⊙O的切线,可得:∠AMP=∠CMP+∠AMB=90°,又∠BAM+∠AMB=90°,可得:∠CMP=∠BAM,∠B=∠C=90°,可证:△ABM≌△MCP,MC=AB,BM=CP,由AD为⊙O的切线,可得:OJ⊥AD,故:JH∥CP,△MOJ∽△MPC,设PD的长为x,则PC=ABx,OJ=![]() PC,OH=ABOJ可求出⊙O的半径,在Rt△MCP中,运用勾股定理可将PD的长求出,即可得出CP的长.
PC,OH=ABOJ可求出⊙O的半径,在Rt△MCP中,运用勾股定理可将PD的长求出,即可得出CP的长.
(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∴∠BAM+∠AMB=90°,
∵∠AMP=90°,
∴∠AMB+∠CMP=90°,
∴∠BAM=∠CMP,
由折叠的性质得:MN垂直平分AP,
∴AM=PM,
在△ABM和△MPC中,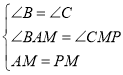 ,
,
∴△ABM≌△MPC(AAS),
∴BM=CP;
(2)解:∵AM是⊙O的切线,
∴∠AMP=90°,
∴∠CMP+∠AMB=90°,
∵∠BAM+∠AMB=90°,
∴∠CMP=∠BAM,
由折叠的性质得:MN垂直平分AP,
∴MA=MP,
∵∠B=∠C=90°,
∴△ABM≌△MCP,
∴MC=AB=4
设PD=x,则CP=4﹣x,
∴BM=PC=4﹣x,
连接HO并延长交BC于J,如图2所示:
∵AD是⊙O的切线,
∴∠JHD=90°,
∴HDCJ为矩形,
∴OJ∥CP,
∴△MOJ∽△MPC,
∴OJ:CP=MO:MP=1:2,
∴OJ=![]() (4﹣x),
(4﹣x),
OH=![]() MP=4﹣OJ=
MP=4﹣OJ=![]() (4+x),
(4+x),
∵MC2=MP2﹣CP2,
∴(4+x)2﹣(4﹣x)2=16,
解得:x=1,即PD=1,
∴PC=3.


科目:初中数学 来源: 题型:
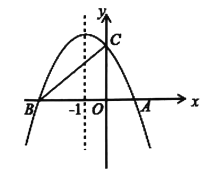
【题目】如图,二次函数![]() 的图象与x轴交于A、B两点,与y轴交于点C,点A的坐标为(2,0),点C的坐标为(0,4),它的对称轴是直线x=-1.
的图象与x轴交于A、B两点,与y轴交于点C,点A的坐标为(2,0),点C的坐标为(0,4),它的对称轴是直线x=-1.
(1)求这个二次函数的解析式;
(2)在第二象限内抛物线上是否存在一点P,使![]() 的面积最大?若存在,求出
的面积最大?若存在,求出![]() 的面积最大值;若没有,请说明理由.
的面积最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.已知线段AB=40cm,点P是线段AB的黄金分割点,且AP>BP,则AP的长约为24.72cm
B.各有一个角是100°的等腰三角形相似
C.所有的矩形都相似
D.菱形既是轴对称图形,又是中心对称图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,连接AC,将![]() 绕点A逆时针旋转α得
绕点A逆时针旋转α得![]() ,连接CF,O为CF的中点,连接OE,OD.
,连接CF,O为CF的中点,连接OE,OD.
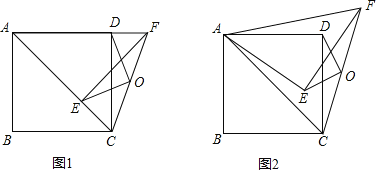
(1)如图1,当![]() 时,请直接写出OE与OD的关系(不用证明).
时,请直接写出OE与OD的关系(不用证明).
(2)如图2,当![]() 时,(1)中的结论是否成立?请说明理由.
时,(1)中的结论是否成立?请说明理由.
(3)当![]() 时,若
时,若![]() ,请直接写出点O经过的路径长.
,请直接写出点O经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 经过点
经过点![]() 、
、![]() 两点,
两点,![]() 是其顶点,将抛物线
是其顶点,将抛物线![]() 绕点
绕点![]() 旋转
旋转![]() ,得到新的抛物线
,得到新的抛物线![]() .
.
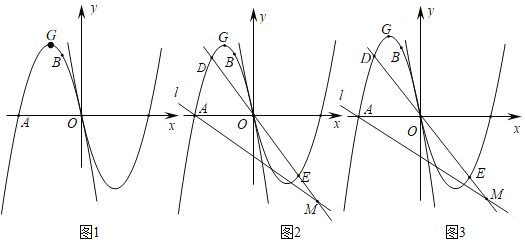
(1)求抛物线![]() 的函数解析式及顶点
的函数解析式及顶点![]() 的坐标;
的坐标;
(2)如图2,直线![]() 经过点
经过点![]() ,
,![]() 是抛物线
是抛物线![]() 上的一点,设
上的一点,设![]() 点的横坐标为
点的横坐标为![]() (
(![]() ),连接
),连接![]() 并延长,交抛物线
并延长,交抛物线![]() 于点
于点![]() ,交直线l于点
,交直线l于点![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)如图3,在(2)的条件下,连接![]() 、
、![]() ,在直线
,在直线![]() 下方的抛物线
下方的抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,
点,![]() .则由抛物线的特征写出如下结论:①
.则由抛物线的特征写出如下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的个数是()
.其中正确的个数是()
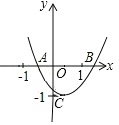
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com