
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛХзЮяЯпЕФЖдГЦжсЮЊжБЯп![]() ЃЌгыyжсИКАыжсНЛгкCЕуЃЌгыxжсНЛгкAЁЂBСНЕуЃЌЦфжаBЕуЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЌЧвOBЃНOCЃЎ
ЃЌгыyжсИКАыжсНЛгкCЕуЃЌгыxжсНЛгкAЁЂBСНЕуЃЌЦфжаBЕуЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЌЧвOBЃНOCЃЎ
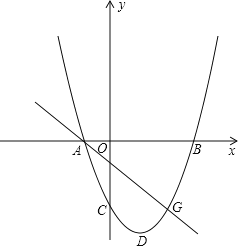
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуGЃЈ2ЃЌyЃЉЪЧИУХзЮяЯпЩЯвЛЕуЃЌЕуPЪЧжБЯпAGЯТЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЌЕБЕуPдЫЖЏЕНЪВУДЮЛжУЪБЃЌЁїAPGЕФУцЛ§зюДѓЃПЧѓГіДЫЪБPЕуЕФзјБъКЭЁїAPGЕФзюДѓУцЛ§.
ЃЈ3ЃЉШєЦНаагкxжсЕФжБЯпгыИУХзЮяЯпНЛгкMЁЂNСНЕуЃЈЦфжаЕуMдкЕуNЕФгвВрЃЉЃЌдкxжсЩЯЪЧЗёДцдкЕуQЃЌЪЙЁїMNQЮЊЕШбќжБНЧШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉPЕуЕФзјБъЮЊ
ЃЛЃЈ2ЃЉPЕуЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ![]() ЃЛЃЈ3ЃЉQЃЈЃ
ЃЛЃЈ3ЃЉQЃЈЃ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЛђЃЈ1ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЛђЃЈ1ЃЌ0ЃЉЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉЩшХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌИљОнвбжЊЕУЕНCЃЈ0ЃЌЉ3ЃЉЃЌAЃЈЉ1ЃЌ0ЃЉЃЌДњШыЕУЕНЗНГЬзщ
ЃЌИљОнвбжЊЕУЕНCЃЈ0ЃЌЉ3ЃЉЃЌAЃЈЉ1ЃЌ0ЃЉЃЌДњШыЕУЕНЗНГЬзщ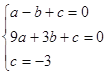 ЃЌЧѓГіЗНГЬзщЕФНтМДПЩЃЛ
ЃЌЧѓГіЗНГЬзщЕФНтМДПЩЃЛ
ЃЈ2ЃЉЙ§ЕуPзїyжсЕФЦНааЯпгыAGНЛгкЕуFЃЌЧѓГіЕуGЕФзјБъЃЈ2ЃЌЉ3ЃЉЃЌЩшжБЯпAGЮЊ![]() ЃЌДњШыЕУЕН
ЃЌДњШыЕУЕН![]() ЃЌЧѓГіЗНГЬзщЕФНтЕУГіжБЯпAGЮЊ
ЃЌЧѓГіЗНГЬзщЕФНтЕУГіжБЯпAGЮЊ![]() ЃЌЩшPЃЈxЃЌ
ЃЌЩшPЃЈxЃЌ![]() ЃЉЃЌдђFЃЈxЃЌЉxЉ1ЃЉЃЌPF
ЃЉЃЌдђFЃЈxЃЌЉxЉ1ЃЉЃЌPF![]() ЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНЧѓГіЁїAPGЕФУцЛ§ЃЌЛЏГЩЖЅЕуЪНМДПЩЃЛ
ЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНЧѓГіЁїAPGЕФУцЛ§ЃЌЛЏГЩЖЅЕуЪНМДПЩЃЛ
ЃЈ3ЃЉДцдкЃЎИљОнMNЁЮxжсЃЌЧвMЁЂNдкХзЮяЯпЩЯЃЌЕУЕНMЁЂNЙигкжБЯпx=1ЖдГЦЃЌЩшЕуMЮЊЃЈmЃЌ![]() ЃЉЧвmЃО1ЃЌЕУЕНMN=2ЃЈmЉ1ЃЉЃЌЕБЁЯQMN=90ЁуЃЌЧвMN=MQЪБЃЌгЩЁїMNQЮЊЕШбќжБНЧШ§НЧаЮЃЌЕУЕН
ЃЉЧвmЃО1ЃЌЕУЕНMN=2ЃЈmЉ1ЃЉЃЌЕБЁЯQMN=90ЁуЃЌЧвMN=MQЪБЃЌгЩЁїMNQЮЊЕШбќжБНЧШ§НЧаЮЃЌЕУЕН![]() ЃЌЧѓГіmЕФжЕЃЌЕУГіЕуMКЭЕуQЕФзјБъЃЛЕБЁЯQNM=90ЁуЃЌЧвMN=NQЪБЃЌЭЌРэПЩЧѓЕуQЕФзјБъЃЌЕБЁЯNQM=90ЁуЃЌЧвMQ=NQЪБЃЌЙ§QзїQEЁЭMNгкЕуEЃЌдђQE=
ЃЌЧѓГіmЕФжЕЃЌЕУГіЕуMКЭЕуQЕФзјБъЃЛЕБЁЯQNM=90ЁуЃЌЧвMN=NQЪБЃЌЭЌРэПЩЧѓЕуQЕФзјБъЃЌЕБЁЯNQM=90ЁуЃЌЧвMQ=NQЪБЃЌЙ§QзїQEЁЭMNгкЕуEЃЌдђQE=![]() MNЃЌИљОнХзЮяЯпМАЕШбќжБНЧШ§НЧаЮЕФжсЖдГЦадЃЌЕУЕНЕуQЕФзјБъЃЎ
MNЃЌИљОнХзЮяЯпМАЕШбќжБНЧШ§НЧаЮЕФжсЖдГЦадЃЌЕУЕНЕуQЕФзјБъЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЩшХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
гЩвбжЊЕУЃКCЃЈ0ЃЌЉ3ЃЉЃЌAЃЈЉ1ЃЌ0ЃЉЃЌ
Ёр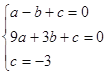 ЃЌНтЕУ
ЃЌНтЕУ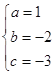 ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЙ§ЕуPзїyжсЕФЦНааЯпгыAGНЛгкЕуQЃЌ
гЩ![]() ЃЌСюx=2ЃЌдђy=Ѓ3ЃЌЁрЕуGЮЊЃЈ2ЃЌЃ3ЃЉЃЌ
ЃЌСюx=2ЃЌдђy=Ѓ3ЃЌЁрЕуGЮЊЃЈ2ЃЌЃ3ЃЉЃЌ
ЩшжБЯпAGЮЊ![]() ЃЌЁр
ЃЌЁр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌМДжБЯпAGЮЊ
ЃЌМДжБЯпAGЮЊ![]() ЃЌ
ЃЌ
ЩшPЃЈxЃЌ![]() ЃЉЃЌдђFЃЈxЃЌЃxЃ1ЃЉЃЌPF
ЃЉЃЌдђFЃЈxЃЌЃxЃ1ЃЉЃЌPF![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
ЁрЕБ![]() ЪБЃЌЁїAPGЕФУцЛ§зюДѓЃЌДЫЪБPЕуЕФзјБъЮЊ
ЪБЃЌЁїAPGЕФУцЛ§зюДѓЃЌДЫЪБPЕуЕФзјБъЮЊ![]() ЃЌ
ЃЌ
ЃЈ3ЃЉДцдкЃЎ
ЁпMNЁЮxжсЃЌЧвMЁЂNдкХзЮяЯпЩЯЃЌЁрMЁЂNЙигкжБЯпx=1ЖдГЦЃЌ
ЩшЕуMЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЧв
ЃЉЧв![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
ЕБЁЯQMN=90ЁуЃЌЧвMN=MQЪБЃЌЁїMNQЮЊЕШбќжБНЧШ§НЧаЮЃЌЁрMQЁЭMNМДMQЁЭxжсЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() Лђ
Лђ![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЈЩсЃЉЛђ
ЃЈЩсЃЉЛђ![]() ЃЌ
ЃЌ![]() ЃЈЩсЃЉЃЌ
ЃЈЩсЃЉЃЌ
ЁрЕуMЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЁрЕуQЮЊЃЈ
ЃЉЃЌЁрЕуQЮЊЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ЕБЁЯQNM=90ЁуЃЌЧвMN=NQЪБЃЌЁїMNQЮЊЕШбќжБНЧШ§НЧаЮЃЌЭЌРэПЩЧѓЕуQЮЊЃЈЃ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ЕБЁЯNQM=90ЁуЃЌЧвMQ=NQЪБЃЌЁїMNQЮЊЕШбќжБНЧШ§НЧаЮЃЌ
Й§QзїQEЁЭMNгкЕуEЃЌдђQE=![]() MNЃЌ
MNЃЌ![]() ЃЌ
ЃЌ
ЁпЗНГЬгаНтЃЌЁргЩХзЮяЯпМАЕШбќжБНЧШ§НЧаЮЕФжсЖдГЦаджЊЕуQЮЊЃЈ1ЃЌ0ЃЉЃЌ
злЩЯЫљЪіЃЌТњзуДцдкТњзуЬѕМўЕФЕуQЃЌЗжБ№ЮЊЃЈЃ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЛђЃЈ1ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЛђЃЈ1ЃЌ0ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§yЃНaЃЈxЉhЃЉ2+kЃЈaЁй0ЃЉЕФЭМЯѓЪЧХзЮяЯпЃЌЖЈвхвЛжжБфЛЛЃЌЯШзїетЬѕХзЮяЯпЙигкдЕуЖдГЦЕФХзЮяЯпyЁфЃЌдйНЋЕУЕНЕФЖдГЦХзЮяЯпyЁфЯђЩЯЦНвЦmЃЈmЃО0ЃЉИіЕЅЮЛЃЌЕУЕНаТЕФХзЮяЯпymЃЌЮвУЧГЦymНазіЖўДЮКЏЪ§yЃНaЃЈxЉhЃЉ2+kЃЈaЁй0ЃЉЕФmНзБфЛЛЃЎ
ЃЈ1ЃЉвбжЊЃКЖўДЮКЏЪ§yЃН2ЃЈx+2ЃЉ2+1ЃЌЫќЕФЖЅЕуЙигкдЕуЕФЖдГЦЕуЮЊЁЁ ЁЁЃЌетИіХзЮяЯпЕФ2НзБфЛЛЕФБэДяЪНЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉШєЖўДЮКЏЪ§MЕФ6НзБфЛЛЕФЙиЯЕЪНЮЊy6ЁфЃНЃЈxЉ1ЃЉ2+5ЃЎ
ЂйЖўДЮКЏЪ§MЕФКЏЪ§БэДяЪНЮЊЁЁ ЁЁЃЎ
ЂкШєЖўДЮКЏЪ§MЕФЖЅЕуЮЊЕуAЃЌгыxжсЯрНЛЕФСНИіНЛЕужазѓВрНЛЕуЮЊЕуBЃЌдкХзЮяЯпy6ЁфЃНЃЈxЉ1ЃЉ2+5ЩЯЪЧЗёДцдкЕуPЃЌЪЙЕуPгыжБЯпABЕФОрРызюЖЬЃЌШєДцдкЃЌЧѓГіДЫЪБЕуPЕФзјБъЃЎ
ЃЈ3ЃЉХзЮяЯпyЃНЉ3x2Љ6x+1ЕФЖЅЕуЮЊЕуAЃЌгыyжсНЛгкЕуBЃЌИУХзЮяЯпЕФmНзБфЛЛЕФЖЅЕуЮЊЕуCЃЎШєЁїABCЪЧвдABЮЊбќЕФЕШбќШ§НЧаЮ,ЧыжБАДаДГіmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌгаСНЬѕЙЋТЗOMЃЌONЯрНЛГЩ30ЁуЃЌбиЙЋТЗOMЗНЯђРыСНЬѕЙЋТЗЕФНЛВцДІOЕу80УзЕФAДІгавЛЫљЯЃЭћаЁбЇЃЌЕБЭЯРЛњбиONЗНЯђааЪЛЪБЃЌОрЭЯРЛњжааФ50УзЕФЗЖЮЇФкОљЛсЪмЕНдывєгАЯьЃЌвбжЊгаСНЬЈЯрОр40УзЕФЭЯРЛње§биONЗНЯђааЪЛЃЌЫќУЧЕФЫйЖШОљЮЊ10Уз/УыЃЌдђетСНЬЈЭЯРЛњбиONЗНЯђааЪЛЪБИјаЁбЇДјРДдывєгАЯьЕФЪБМфЮЊ ЃЈ ЃЉ
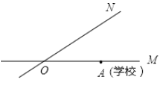
A. 6УыB. 8УыC. 10УыD. 18Уы
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧХзЮяЯпаЭЙАЧХЃЌЕБЙАЖЅРыЫЎУц2mЪБЃЌЫЎУцПэ4mЃЌЫЎУцЯТНЕ2mЃЌЫЎУцПэЖШдіМг______m.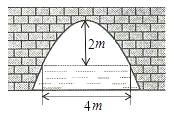
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЁїABCФкНггкЁбOЃЌOHЁЭACгкHЃЌЙ§AЕуЕФЧаЯпгыOCЕФбгГЄЯпНЛгкЕуDЃЌЁЯBЃН30ЁуЃЌOHЃН5![]() ЃЎ
ЃЎ
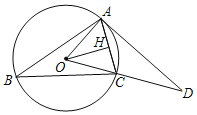
ЃЈ1ЃЉЧѓЁбOЕФАыОЖЃЛ
ЃЈ2ЃЉЧѓГіСгЛЁACЕФГЄЃЈНсЙћБЃСєІаЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
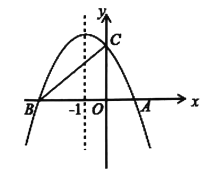
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌЕуAЕФзјБъЮЊ(2ЃЌ0)ЃЌЕуCЕФзјБъЮЊ(0ЃЌ4)ЃЌЫќЕФЖдГЦжсЪЧжБЯпx=-1.
ЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌЕуAЕФзјБъЮЊ(2ЃЌ0)ЃЌЕуCЕФзјБъЮЊ(0ЃЌ4)ЃЌЫќЕФЖдГЦжсЪЧжБЯпx=-1.
(1)ЧѓетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
(2)дкЕкЖўЯѓЯоФкХзЮяЯпЩЯЪЧЗёДцдквЛЕуPЃЌЪЙ![]() ЕФУцЛ§зюДѓЃПШєДцдкЃЌЧѓГі
ЕФУцЛ§зюДѓЃПШєДцдкЃЌЧѓГі![]() ЕФУцЛ§зюДѓжЕЃЛШєУЛгаЃЌЧыЫЕУїРэгЩ.
ЕФУцЛ§зюДѓжЕЃЛШєУЛгаЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈВЛе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A.вбжЊЯпЖЮABЃН40cmЃЌЕуPЪЧЯпЖЮABЕФЛЦН№ЗжИюЕуЃЌЧвAPЃОBPЃЌдђAPЕФГЄдМЮЊ24.72cm
B.ИїгавЛИіНЧЪЧ100ЁуЕФЕШбќШ§НЧаЮЯрЫЦ
C.ЫљгаЕФОиаЮЖМЯрЫЦ
D.СтаЮМШЪЧжсЖдГЦЭМаЮЃЌгжЪЧжааФЖдГЦЭМаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЁЂ
ЁЂ![]() СНЕуЃЌ
СНЕуЃЌ![]() ЪЧЦфЖЅЕуЃЌНЋХзЮяЯп
ЪЧЦфЖЅЕуЃЌНЋХзЮяЯп![]() ШЦЕу
ШЦЕу![]() а§зЊ
а§зЊ![]() ЃЌЕУЕНаТЕФХзЮяЯп
ЃЌЕУЕНаТЕФХзЮяЯп![]() ЃЎ
ЃЎ
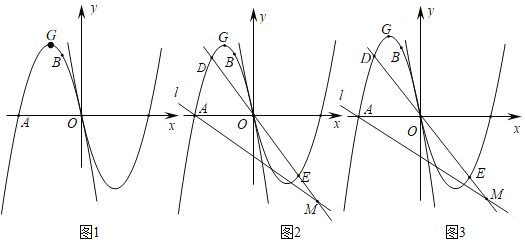
ЃЈ1ЃЉЧѓХзЮяЯп![]() ЕФКЏЪ§НтЮіЪНМАЖЅЕу
ЕФКЏЪ§НтЮіЪНМАЖЅЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌжБЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌ
ЃЌ![]() ЪЧХзЮяЯп
ЪЧХзЮяЯп![]() ЩЯЕФвЛЕуЃЌЩш
ЩЯЕФвЛЕуЃЌЩш![]() ЕуЕФКсзјБъЮЊ
ЕуЕФКсзјБъЮЊ![]() ЃЈ
ЃЈ![]() ЃЉЃЌСЌНг
ЃЉЃЌСЌНг![]() ВЂбгГЄЃЌНЛХзЮяЯп
ВЂбгГЄЃЌНЛХзЮяЯп![]() гкЕу
гкЕу![]() ЃЌНЛжБЯпlгкЕу
ЃЌНЛжБЯпlгкЕу![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌдкжБЯп
ЃЌдкжБЯп![]() ЯТЗНЕФХзЮяЯп
ЯТЗНЕФХзЮяЯп![]() ЩЯЪЧЗёДцдкЕу
ЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃПШєДцдкЃЌЧѓГіЕу
ЃПШєДцдкЃЌЧѓГіЕу![]() ЕФКсзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФКсзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЪЧБп
ЪЧБп![]() ЩЯЕФвЛЖЏЕуЃЈВЛгыЕу
ЩЯЕФвЛЖЏЕуЃЈВЛгыЕу![]() ЃЌ
ЃЌ![]() жиКЯЃЉЃЌСЌНг
жиКЯЃЉЃЌСЌНг![]() ЃЌЕу
ЃЌЕу![]() ЙигкжБЯп
ЙигкжБЯп![]() ЕФЖдГЦЕуЮЊ
ЕФЖдГЦЕуЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() ВЂбгГЄНЛ
ВЂбгГЄНЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
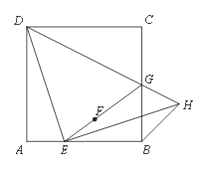
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉгУЕШЪНБэЪОЯпЖЮ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЎ
ЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЎ
ЃЈ3ЃЉШєе§ЗНаЮ![]() ЕФБпГЄЮЊ4ЃЌШЁDHЕФжаЕуMЃЌЧыжБНгаДГіЯпЖЮBMГЄЕФзюаЁжЕЁЃ
ЕФБпГЄЮЊ4ЃЌШЁDHЕФжаЕуMЃЌЧыжБНгаДГіЯпЖЮBMГЄЕФзюаЁжЕЁЃ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com