
����Ŀ�����κ���y��a��x��h��2+k��a��0����ͼ���������ߣ�����һ�ֱ任���������������߹���ԭ��ԳƵ�������y�䣬�ٽ��õ��ĶԳ�������y������ƽ��m��m��0������λ���õ��µ�������ym�����dz�ym�������κ���y��a��x��h��2+k��a��0����m�ױ任��
��1����֪�����κ���y��2��x+2��2+1�����Ķ������ԭ��ĶԳƵ�Ϊ�� ������������ߵ�2�ױ任�ı���ʽΪ�� ����
��2�������κ���M��6�ױ任�Ĺ�ϵʽΪy6�䣽��x��1��2+5��
�����κ���M�ĺ�������ʽΪ�� ����
�������κ���M�Ķ���Ϊ��A����x���ཻ��������������ཻ��Ϊ��B����������y6�䣽��x��1��2+5���Ƿ���ڵ�P��ʹ��P��ֱ��AB�ľ�����̣������ڣ������ʱ��P�����꣮
��3��������y����3x2��6x+1�Ķ���Ϊ��A����y�ύ�ڵ�B���������ߵ�m�ױ任�Ķ���Ϊ��C������ABC����ABΪ���ĵ���������,��ֱ��д��m��ֵ��
���𰸡���1����2����1����y����2��x��2��2��1����2�����ڣ���P��![]() ��
��![]() ������3��8+
������3��8+![]() ��8��
��8��![]() ��8��2��
��8��2��
��������
��1��ԭ���κ����Ķ���Ϊ��-2��1���������ԭ��ĶԳƵ�Ϊ��2��-1����������⣻��2����6�ױ任�Ĺ�ϵʽ��Ӧ�ĺ�������Ϊ����1��-1��������M�Ķ���Ϊ����-1��1����������⣻��DP =![]() PH=
PH=![]() ��x2-2x+6-x-2��=
��x2-2x+6-x-2��=![]() ��x2-3x+4����������⣻
��x2-3x+4����������⣻
��3����A��-1��4������B��0��1���������ߵ�m�ױ任�ĺ�������ʽΪ��y=3��x-1��2-4+m���ʵ�C��1��m-4����������⣮
�⣺��1��ԭ���κ����Ķ���Ϊ����2��1���������ԭ��ĶԳƵ�Ϊ��2����1����
����������ߵ�2�ױ任�ı���ʽ��y����2��x��2��2��1��
�ʴ�Ϊ����2����1����y����2��x��2��2��1��
��2����6�ױ任�Ĺ�ϵʽ��Ӧ�ĺ�������Ϊ����1����1��������M�Ķ���Ϊ������1��1����
�������ʽΪ��y������x+1��2+1��
�ʴ�Ϊ��y������x+1��2+1��
�����ڣ����ɣ�
y������x+1��2+1����y��0����x����2��0��
�ʵ�B����2��0��������A����1��1����
����A��B���������һ�κ�������ʽ��y��kx+b�ã�![]() ����ã�
����ã�![]() ��
��
��ֱ��AB�ĺ�������ʽΪ��y��x+2��
y6�䣽��x��1��2+5��x2��2x+6��
����ͼ������P��PD��AB���ڵ�D���ʵ�P��y���ƽ���߽�AB�ڵ�H��
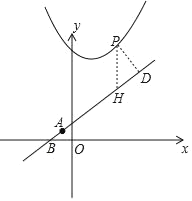
��ֱ��AB����б��Ϊ45�㣬��DP��![]() PH��
PH��
���P��x��x2��2x+6�������H��x��x+2����
DP��![]() PH��
PH��![]() ��x2��2x+6��x��2����
��x2��2x+6��x��2����![]() ��x2��3x+4����
��x2��3x+4����
��![]() ��0����DP����Сֵ����ʱx��
��0����DP����Сֵ����ʱx��![]() ��
��
�ʵ�P��![]() ��
��![]() ����
����
��3��������y����3x2��6x+1�Ķ���Ϊ��A����y�ύ�ڵ�B��
���A����1��4������B��0��1����
�����ߵ�m�ױ任�ĺ�������ʽΪ��y��3��x��1��2��4+m��
�ʵ�C��1��m��4����
��AB2��10��AC2��4+��m��8��2��BC2��1+��m��5��2��
��AB��ACʱ��10��4+��m��8��2����ã�m��8![]() ��
��
��AB��BCʱ��ͬ���ɵã�m��8��2��
��m��ֵΪ��8+![]() ��8��
��8��![]() ��8��2��
��8��2��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
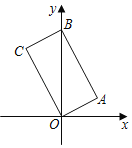
����Ŀ����ͼ���ı���OABC�Ǿ��Σ�A(2��1)��B(0��5)����C�ڵڶ����ޣ����C��������______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ���㣨-2��-3���͵㣨1��6��
���㣨-2��-3���͵㣨1��6��
��1������������Ľ���ʽ��
��2����![]() ��ʲô��Χ��ʱ������ֵ
��ʲô��Χ��ʱ������ֵ![]() ��
��![]() �����������
�����������
��3�������������ͼ����![]() ��Ľ�������.
��Ľ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
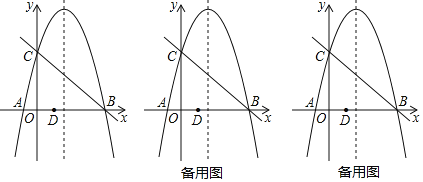
����Ŀ����ͼ��������y=ax2+4x+c��x�ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��y=-x+5������B��C��
��1���������ߵı���ʽ��
��2����D��1��0������PΪ�Գ�����һ���㣬����BP��CP��
������CPB=90�������P�����ꣻ
�ڵ�QΪ��������һ���㣬����C��D��P��QΪ������ı�����ƽ���ı��Σ���P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ڿ�չ���齻����У�ȫ��ʦ���������飬Ϊ�˽������鼮�����࣬�Բ�����ݽ����˳������飬����ʦ���ݵ������ݻ��������²�������ͳ��ͼ�������ͳ��ͼ�ش��������⣺
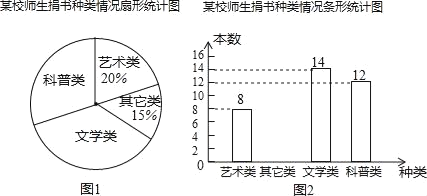
��1������������������ ������
��2��������ͳ��ͼ����������
��3�����λʦ��������1600��������ƿ������鼮�ı�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼ������������Ŀڴ��У��ֱ��д�С��������ȫ��ͬ��С�����мڴ��е�С���Ϸֱ��������1��2��3��4���ҿڴ��е�С���Ϸֱ��������2��3��4���ȴӼ״�����������һ��С��������Ϊm���ٴ��Ҵ�������һ��С��������Ϊn��
��1�������б�����״ͼ�ķ�����ʾ�����У�m��n�����ܵĽ����
��2����m��n���Ƿ���x2��5x+6��0�Ľ�ʱ����С����ʤ����m��n�����Ƿ���x2��5x+6��0�Ľ�ʱ����С����ʤ������������˭��ʤ�ĸ��ʴ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������һ�鳤50m����30m�ľ��οյؽ��ɾ������㳡����Ʒ�����ͼ����Ӱ����Ϊ�̻������Ŀ��̻���Ϊ��С����״����ͬ�ľ��Σ����հ�����Ϊ����������ܵ�4�����ڿ�����ͬ�����̻����ϳ���xΪ��ֵʱ�����������ﵽ1341m2��
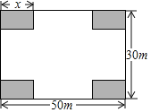
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�E��F�ֱ���BC��CD�ϵĵ㣬�ҡ�EAF��45����AE��AF�ֱ�BD��M��N������EN��EF�������½��ۣ���AN��EN���ڵ�AE��AFʱ��![]() ��2��
��2��![]() ����BE+DF��EF���ܴ��ڵ�E��F��ʹ��NF��DF��������ȷ�ĸ����ǣ�������
����BE+DF��EF���ܴ��ڵ�E��F��ʹ��NF��DF��������ȷ�ĸ����ǣ�������
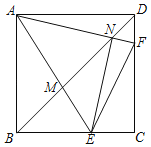
A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�����ߵĶԳ���Ϊֱ��![]() ����y�Ḻ���ύ��C�㣬��x�ύ��A��B���㣬����B�������Ϊ��3��0������OB��OC��
����y�Ḻ���ύ��C�㣬��x�ύ��A��B���㣬����B�������Ϊ��3��0������OB��OC��
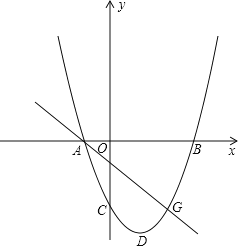
��1����������ߵĽ���ʽ��
��2������G��2��y���Ǹ���������һ�㣬��P��ֱ��AG�·�����������һ���㣬����P�˶���ʲôλ��ʱ����APG�������������ʱP����������APG��������.
��3����ƽ����x���ֱ����������߽���M��N���㣨���е�M�ڵ�N���Ҳࣩ����x�����Ƿ���ڵ�Q��ʹ��MNQΪ����ֱ�������Σ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com