
【题目】台州人民翘首以盼的乐清湾大桥于2018年9月28日正式通车,经统计分析,大桥上的车流速度![]() (千米/小时)是车流密度
(千米/小时)是车流密度![]() (辆/千米)的函数,当桥上的车流密度达到220辆/千米的时候就造成交通堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米,车流速度为80千米/小时,研究证明:当
(辆/千米)的函数,当桥上的车流密度达到220辆/千米的时候就造成交通堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米,车流速度为80千米/小时,研究证明:当![]() 时,车流速度
时,车流速度![]() 是车流密度
是车流密度![]() 的一次函数.
的一次函数.
(1)求大桥上车流密度为50/辆千米时的车流速度;
(2)在某一交通高峰时段,为使大桥上的车流速度大于60千米/小时且小于80千米/小时,应把大桥上的车流密度控制在什么范围内?
(3)车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量![]() 车流速度
车流速度![]() 车流密度,求大桥上车流量
车流密度,求大桥上车流量![]() 的最大值.
的最大值.
【答案】(1)车流速度68千米/小时;(2)应把大桥上的车流密度控制在20千米/小时到70千米/小时之间;(3)车流量y取得最大值是每小时4840辆
【解析】
(1)设车流速度![]() 与车流密度
与车流密度![]() 的函数关系式为v=kx+b,列式求出函数解析式,将x=50代入即可得到答案;
的函数关系式为v=kx+b,列式求出函数解析式,将x=50代入即可得到答案;
(2)根据题意列不等式组即可得到答案;
(3)分两种情况:![]() 、
、![]() 时分别求出y的最大值即可.
时分别求出y的最大值即可.
(1)设车流速度![]() 与车流密度
与车流密度![]() 的函数关系式为v=kx+b,由题意,得
的函数关系式为v=kx+b,由题意,得
![]() ,
,
解得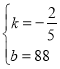 ,
,
∴当![]() 时,车流速度
时,车流速度![]() 是车流密度
是车流密度![]() 的一次函数为
的一次函数为![]() ,
,
当x=50时,![]() (千米/小时),
(千米/小时),
∴大桥上车流密度为50/辆千米时的车流速度68千米/小时;
(2)由题意得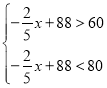 ,
,
解得20<x<70,符合题意,
∴为使大桥上的车流速度大于60千米/小时且小于80千米/小时,应把大桥上的车流密度控制在20千米/小时到70千米/小时之间;
(3)由题意得y=vx,
当![]() 时,y=80x,
时,y=80x,
∵k=80>0,
∴y随x的增大而增大,
∴当x=20时,y有最大值1600,
当![]() 时,
时,
y![]() ,
,
当x=110时,y有最大值4840,
∵4840>1600,
∴当车流密度是110辆/千米,车流量y取得最大值是每小时4840辆.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=-x2+bx+c经过点(0,6),其对称轴为直线x=![]() .在x轴上方作平行于x轴的直线l与抛物线交于A、B两点(点A在对称轴的右侧),过点A、B作x轴的垂线,垂足分别为D、C.设A点的横坐标为m.
.在x轴上方作平行于x轴的直线l与抛物线交于A、B两点(点A在对称轴的右侧),过点A、B作x轴的垂线,垂足分别为D、C.设A点的横坐标为m.

(1)求此抛物线所对应的函数关系式.
(2)当m为何值时,矩形ABCD为正方形.
(3)当m为何值时,矩形ABCD的周长最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
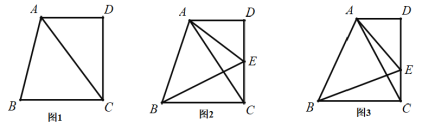
【题目】问题提出:
(1)如图1,在四边形![]() 中,已知:
中,已知:![]() ,
,![]() ,
,![]() ,
,![]() 的面积为8,求
的面积为8,求![]() 边上的高.
边上的高.
问题探究
(2)如图2在(1)的条件下,点![]() 是
是![]() 边上一点,且
边上一点,且![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的面积
的面积
问题解决
(3)如图3,在(1)的条件下,点![]() 是
是![]() 边上任意一点,连接
边上任意一点,连接![]() 、
、![]() ,若
,若![]() ,
,![]() 的面积是否存在最小值;若存在,求出最小值;若不存在;请说明理由.
的面积是否存在最小值;若存在,求出最小值;若不存在;请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
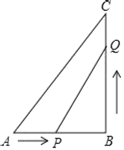
【题目】已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发.
(1)几秒后,△PBQ的面积等于6cm2?
(2)几秒后,四边形APQC的面积最小?最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 请画出△ABC关于原点对称的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商场经销一种高档水果,商场为了在中秋节和国庆节期间扩大销量,将售价从原来的每千克40元经两次调价后调至每千克32.4元.
(1)若该商场两次调次的降价率相同,求这个降价率;
(2)现在假期结束了,商场准备适当涨价,如果现在每千克盈利10元,每天可售出500千克,经市场调查发现,在进货不变的情况下,若每千克涨价1元,日销量将减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元;
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
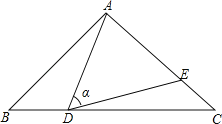
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=![]() ,下列结论:
,下列结论:
①△ADE∽△ACD;
②当BD=6时,△ABD与△DCE全等;
③当△DCE为直角三角形时,BD为8或![]() ;
;
④0<CE≤6.4.
其中正确的结论是( )
A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com