
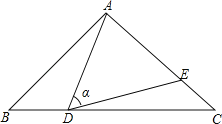
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=![]() ,下列结论:
,下列结论:
①△ADE∽△ACD;
②当BD=6时,△ABD与△DCE全等;
③当△DCE为直角三角形时,BD为8或![]() ;
;
④0<CE≤6.4.
其中正确的结论是( )
A.①②③B.①②④C.①③④D.①②③④
【答案】D
【解析】
①先证明∠B=∠C,从而可得出∠ADE=∠C,又∠DAE=∠CAD可得出结论;②作AG⊥BC于G,先求出BG的长,从而可得出BC的长,再得出DC=10=AB,可由ASA证明△ABD≌△DCE;③分两种情况:当∠AED=90°时,由①知△ADE∽△ACD,从而有∠ADC=∠AED=90°,则有BD=CD,最后∠ADE=∠B=α且cosα=![]() 可得出BD的长;当∠CDE=90°时,易△CDE∽△BAD,则∠CDE=90°=∠BAD,最后根据cosα=cosB=
可得出BD的长;当∠CDE=90°时,易△CDE∽△BAD,则∠CDE=90°=∠BAD,最后根据cosα=cosB=![]() 可得出结果;④先证明△CDE∽△BAD,由②可知BC=16,设BD=y,CE=x,得
可得出结果;④先证明△CDE∽△BAD,由②可知BC=16,设BD=y,CE=x,得![]()
![]() ,即
,即![]() ,然后可得出y与x之间的关系式为(y﹣8)2=64﹣10x,从而可得出结果.
,然后可得出y与x之间的关系式为(y﹣8)2=64﹣10x,从而可得出结果.
解:①∵AB=AC,∴∠B=∠C,又∵∠ADE=∠B,∴∠ADE=∠C,又∠DAE=∠CAD,∴△ADE∽△ACD,故①正确;
②作AG⊥BC于G,∵AB=AC=10,∴BC=2BG,又∠ADE=∠B=α,cosα=![]() ,∴BG=ABcosα=8,∴BC=2BG==16,∵BD=6,∴DC=10,∴AB=DC,又∠ADC=∠B+∠BAD=∠ADE+∠CDE,又∠B=∠ADE,∴∠BAD=∠CDE,在△ABD与△DCE中,
,∴BG=ABcosα=8,∴BC=2BG==16,∵BD=6,∴DC=10,∴AB=DC,又∠ADC=∠B+∠BAD=∠ADE+∠CDE,又∠B=∠ADE,∴∠BAD=∠CDE,在△ABD与△DCE中,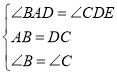 ,∴△ABD≌△DCE(ASA),故②正确;
,∴△ABD≌△DCE(ASA),故②正确;

③当∠AED=90°时,由①可知:△ADE∽△ACD,∴∠ADC=∠AED,∵∠AED=90°,∴∠ADC=90°,即AD⊥BC,∵AB=AC,∴BD=CD,∴∠ADE=∠B=α且cosα=![]() ,AB=10,BD=8;当∠CDE=90°时,易△CDE∽△BAD,∵∠CDE=90°,∴∠BAD=90°,∵∠B=α且cosα=
,AB=10,BD=8;当∠CDE=90°时,易△CDE∽△BAD,∵∠CDE=90°,∴∠BAD=90°,∵∠B=α且cosα=![]() ,AB=10,∴cosB=
,AB=10,∴cosB=![]()
![]() ,∴BD=
,∴BD=![]() ,故③正确;
,故③正确;
④易证得△CDE∽△BAD,由②可知BC=16,设BD=y,CE=x,∴![]()
![]() ,∴
,∴![]() ,整理得:y2﹣16y+64=64﹣10x,即(y﹣8)2=64﹣10x,∴0<x≤6.4,故④正确;
,整理得:y2﹣16y+64=64﹣10x,即(y﹣8)2=64﹣10x,∴0<x≤6.4,故④正确;
故选:D.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】台州人民翘首以盼的乐清湾大桥于2018年9月28日正式通车,经统计分析,大桥上的车流速度![]() (千米/小时)是车流密度
(千米/小时)是车流密度![]() (辆/千米)的函数,当桥上的车流密度达到220辆/千米的时候就造成交通堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米,车流速度为80千米/小时,研究证明:当
(辆/千米)的函数,当桥上的车流密度达到220辆/千米的时候就造成交通堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米,车流速度为80千米/小时,研究证明:当![]() 时,车流速度
时,车流速度![]() 是车流密度
是车流密度![]() 的一次函数.
的一次函数.
(1)求大桥上车流密度为50/辆千米时的车流速度;
(2)在某一交通高峰时段,为使大桥上的车流速度大于60千米/小时且小于80千米/小时,应把大桥上的车流密度控制在什么范围内?
(3)车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量![]() 车流速度
车流速度![]() 车流密度,求大桥上车流量
车流密度,求大桥上车流量![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,C为⊙O上一点,∠OAC=58°.
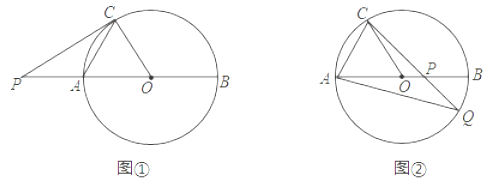
(Ⅰ)如图①,过点C作⊙O的切线,与BA的延长线交于点P,求∠P的大小;
(Ⅱ)如图②,P为AB上一点,CP延长线与⊙O交于点Q.若AQ=CQ,求∠APC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若数a使关于x的不等式组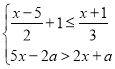 至少有3个整数解,且使关于y的分式方程
至少有3个整数解,且使关于y的分式方程![]() =2有非负整数解,则满足条件的所有整数a的和是( )
=2有非负整数解,则满足条件的所有整数a的和是( )
A. 14B. 15C. 23D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会为了解本校九年级学生体育测试中跳小绳成的情况,随机抽取了该校九年级若干名学生,调查他们的跳小绳成绩![]() (次1分),按成绩分成
(次1分),按成绩分成![]() ,
,![]() ,
,![]() ,
,![]() 五个等级.在本次调查中,男、女生的人数相同将所得数据绘制成如下的统计图:
五个等级.在本次调查中,男、女生的人数相同将所得数据绘制成如下的统计图:
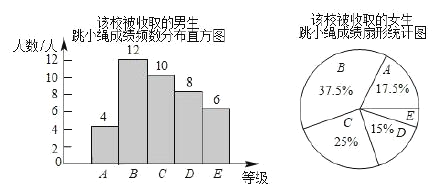
根据以上统计图提供的信息,解答下列问题:
(1)本次调查中,男生的跳小绳成绩的中位数在 等级;
(2)求本次调查中女生的跳小绳成绩为![]() 等级的人数:
等级的人数:
(3)若该校九年级共有男生400人,女生380人,估计该校九年级学生跳小绳成绩为![]() 等级的人数.
等级的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
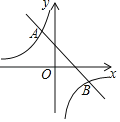
【题目】如图,一次函数y=k1x+b(k1≠0)与反比例函数y=![]() (k2≠0)的图象交于点A(﹣1,2),B(m,﹣1).
(k2≠0)的图象交于点A(﹣1,2),B(m,﹣1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0)(n>0),使△ABP为等腰三角形?若存在,求n的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
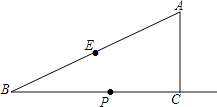
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
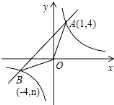
【题目】已知:如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() .
.
(1)求一次函数和反比例函数的解析式;
(2)求![]() 的面积;
的面积;
(3)根据图象,试比较![]() ,
,![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+mx﹣n的对称轴为x=2.若关于x的一元二次方程x2+mx﹣n=0在﹣1<x<6的范围内有实数解,则n的取值范围是( )
A.﹣4≤n<5B.n≥﹣4C.﹣4≤n<12D.5<n<12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com