【题目】二次函数y＝x2+mx﹣n的对称轴为x＝2．若关于x的一元二次方程x2+mx﹣n＝0在﹣1＜x＜6的范围内有实数解，则n的取值范围是（ ）
A.﹣4≤n＜5B.n≥﹣4C.﹣4≤n＜12D.5＜n＜12
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC=10，点D是边BC上一动点(不与B，C重合)，∠ADE=∠B=α，DE交AC于点E，且cosα=
，下列结论：
①△ADE∽△ACD；
②当BD=6时，△ABD与△DCE全等；
③当△DCE为直角三角形时，BD为8或
；
④0＜CE≤6.4．
其中正确的结论是( )
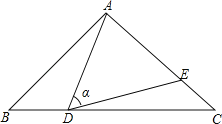
A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y=ax2+bx+c的x，y的部分对应值如表所示，则下列判断不正确的是（ ）
x | ﹣2 | ﹣1 | 0 | 1 | 2 |
y | ﹣2.5 | 0 | 1.5 | 2 | 1.5 |
A.当x＜0时，y随x的增大而增大
B.对称轴是直线x=1
C.当x=4时，y=﹣2
D.方程ax2+bx+c=0有一个根是3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，
，
，
是线段
上的点，
是线段
上的点，且
．
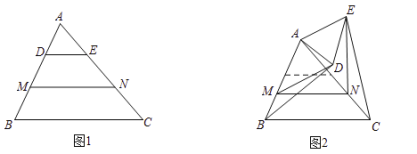
（1）观察猜想
如图1，若点是线段的三等分点，则
__________，
___________．由此，我们猜想线段
，
，
，
之间满足的数量关系是_________．
（2）类比探究
将
在平面内绕点
按逆时针方向旋转一定的角度，连接，
，，
，猜想在旋转的过程中，（1）中的结论是否仍然成立？若成立，请仅就图2的情形给出证明；若不成立，请说明理由．
（3）解决问题
将在平面内绕点自由旋转，若
，请直接写出线段
的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了落实党的“精准扶贫”政策，A、B两城决定向C、D两乡运送肥料以支持农村生产，已知A、B两城共有肥料500吨，其中A城肥料比B城少100吨，从A、B城往C、D两乡运肥料的平均费用如下表. 现C乡需要肥料240吨，D乡需要肥料260吨.
A城(出) | B城(出) | |
C乡(人) | 20元/吨 | 15元/吨 |
D乡(人) | 25元/吨 | 30元/吨 |
（1）A城和B城各多少吨肥料？
（2）设从B城运往D乡肥料x吨，总运费为y元，求y与x之间的函数关系，并写出自变量x的取值范围；
（3）由于更换车型，使B城运往D乡的运费每吨减少a元(a＞0)，其余路线运费不变，若C、D两乡的总运费最小值不少于10040元，求a的最大整数值.
查看答案和解析>>
科目：初中数学 来源： 题型：
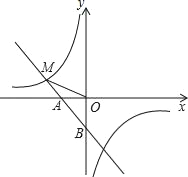
【题目】如图，一次函数y1＝﹣x﹣1的图象与x轴交于点A，与y轴交于点B，与反比例函数
图象的一个交点为M（﹣2，m）．
（1）求反比例函数的解析式；
（2）当y2＞y1时，求x的取值范围；
（3）求点B到直线OM的距离．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
